
Conclusivo prima di un esame di certificazione
|
You must specify a text. |
|
|
You must specify a date. |

.
<title> personalizzato: “Modulo iscrizione corso RIM”.<header> con il nome della scuola e un breve slogan.<h1> con il titolo del modulo e un’emoji decorativa.<fieldset> con <legend> “Dati personali”.nome, cognome, email, telefono.required sui campi obbligatori.placeholder esplicativi per ogni campo.date per la data di nascita.number per indicare l’età.<select> per la “Regione di provenienza” (almeno 5 regioni).url per indicare un eventuale sito personale.email con controllo di formato.color per far scegliere il colore preferito.range per valutare il livello di conoscenza informatica (0–10).search per cercare corsi disponibili.<datalist> collegato con almeno 5 opzioni di corsi.select per indicare il “Corso scelto” con almeno 3 opzioni.<select multiple> per “Lingue conosciute” (es. Italiano, Inglese, Spagnolo, Francese).<textarea> per “Motivazioni dell’iscrizione” (almeno 4 righe).file per caricare un documento d’identità.accept=".pdf,.jpg,.png".hidden con un codice utente fisso.number per “Anni di esperienza scolastica”.month per indicare il “Mese di inizio corso”.week per indicare la “Settimana di frequenza”.time per indicare l’orario preferito delle lezioni.datetime-local per la data e ora di iscrizione.tel per un secondo recapito telefonico.url per un eventuale profilo LinkedIn.submit con etichetta “Invia iscrizione”.reset con etichetta “Cancella dati”.button con testo “Verifica dati” (senza JavaScript).<fieldset> separato con titolo “Conferma finale”.output (vuoto) per eventuali risultati calcolati.<footer> con il nome dell’autore e la data di creazione del file.👉 Consegna:
Salva il file come modulo_iscrizione.html e assicurati che tutti i campi e gli attributi funzionino correttamente nel browser.
Valore complessivo: 40 punti (1 punto per ogni richiesta).
Basandosi sul documento excel che si allega si risponda alle relative domande
Raccoltaesercizisemplici (3) (1) (1) (2) (1)
|
You must specify a text. |
|
|
You must specify a date. |

Codice Dart su Flutter per la visualizzazione di un pulsante:
import 'package:flutter/material.dart';
void main() {
runApp(const MyApp());
}
class MyApp extends StatelessWidget {
const MyApp({super.key});
@override
Widget build(BuildContext context) {
return MaterialApp(
title: 'Esempio Pulsante',
home: const ContatorePage(),
);
}
}
class ContatorePage extends StatefulWidget {
const ContatorePage({super.key});
@override
State<ContatorePage> createState() => _ContatorePageState();
}
class _ContatorePageState extends State<ContatorePage> {
int _contatore = 0;
void _incrementa() {
setState(() {
_contatore++;
});
}
@override
Widget build(BuildContext context) {
return Scaffold(
appBar: AppBar(
title: const Text('Pulsante con risultato a schermo'),
),
body: Center(
child: Column(
mainAxisAlignment: MainAxisAlignment.center,
children: [
Text(
'Hai premuto il pulsante $_contatore volte',
style: const TextStyle(fontSize: 20),
),
const SizedBox(height: 20),
ElevatedButton(
onPressed: _incrementa,
child: const Text("Premi qui"),
),
],
),
),
);
}
}
L’esito è il seguente:
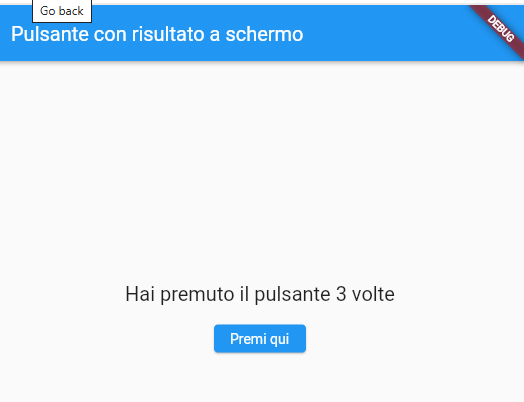
Il concetto di classe è quello tradizionale con il concetto di metodi ed oggetti.
Il metodo è associato al concetto di funzione, l’oggetto è collegato con il concetto di variabile.
Ecco un esempio:
class Persona {
// Attributi (variabili di istanza)
String nome;
int eta;
// Costruttore
Persona(this.nome, this.eta);
// Metodo della classe
void saluta() {
print("Ciao, mi chiamo $nome e ho $eta anni.");
}
}
void main() {
// Creazione di un oggetto di tipo Persona
Persona p = Persona("Francesco", 35);
// Chiamata al metodo dell'oggetto
p.saluta(); // Output: Ciao, mi chiamo Francesco e ho 35 anni.
}
Ecco un esempio con metodo ed attributo:
class Auto {
// Attributo
String marca;
// Costruttore
Auto(this.marca);
// Metodo
void accendiMotore() {
print("L'auto $marca è accesa!");
}
}
void main() {
// Creazione di un oggetto della classe Auto
var miaAuto = Auto("Fiat");
// Uso dell’attributo
print("La mia auto è una ${miaAuto.marca}");
// Chiamata del metodo
miaAuto.accendiMotore();
}
Prima di passare al concetto di ereditarietà voglio evidenziare che se il concetto di costruttore esiste, non esiste il concetto di distruttore.
Vi è il concetto di garbage collection ossia della liberazione della memoria attraverso un processo aleatorio.
Ecco una tabella per confrontare linguaggi, tempo di sviluppo, Performance e gestione della memoria.
| Programma | Sviluppo | Performance | Memoria |
| Dart | molto rapido | sufficiente meno intuitivo per calcolo intensivo | GC |
| Kotlin | buono | buona | GC |
| Java | buono | buona | GC |
| C# | buona | buona | GC |
| Rust | complesso | molto buona | Ownership |
La mia riflessione porta ad affermare che, per favorire la velocità di sviluppo, non si pone più l’attenzione verso l’uso della memoria che viene alla fine usata dai singoli dispositivi mobili.
Esempio di ereditarietà fondamentale poi per apprendere le estensioni delle classi in Flutter:
// Classe base
class Persona {
String nome;
int eta;
Persona(this.nome, this.eta);
void saluta() {
print("Ciao, mi chiamo $nome e ho $eta anni.");
}
}
// Classe derivata che estende Persona
class Studente extends Persona {
String corsoDiStudi;
// Costruttore della classe derivata che chiama il costruttore base
Studente(String nome, int eta, this.corsoDiStudi) : super(nome, eta);
// Metodo aggiuntivo
void studia() {
print("$nome sta studiando $corsoDiStudi.");
}
Il vero e proprio percorso comincia da qui dopo aver visto la potenzialità del framework Flutter.
Comincio con le definizioni classiche.
Ambiente di sviluppo: dartpad.dev
I Esempio – stampa a video “Hello Word”
void main() {
print("Hello word");
}
Si nota subito che se si sbaglia a digitare il codice subito interviene l’interprete on line, non serve compilare!
Non si deve includere alcuna libreria per scrivere in output.
II esempio – costrutto if then else
void main() {
int numero = 5;
if (numero > 0) {
print("Il numero è positivo");
} else {
print("Il numero è zero o negativo");
}
}
non esiste la parola then come in altri linguaggi
III esempio – costrutto while
void main() {
int numero = 1;
while (numero <= 5) {
print('Numero: $numero');
numero++;
}
print('Fine ciclo');
}
IV esempio costrutto for
void main() {
// Ciclo for che conta da 1 a 5
for (int i = 1; <= 5; i++) {
print('Numero: $i');
}
}
V esempio gestione vettore e matrici molto simile a Python
void main() {
// Creazione di un "vettore" (lista) di interi
List<int> numeri = [10, 20, 30, 40];
// Aggiungere un elemento
numeri.add(50);
// Accedere a un elemento (indice parte da 0)
print(numeri[0]); // 10
// Modificare un elemento
numeri[1] = 25;
// Ciclo for per stampare tutti gli elementi
for (int n in numeri) {
print(n);
}
// Lunghezza del vettore
print("Lunghezza: ${numeri.length}");
}
void main() {
// Definisco una matrice 3x3
List<List<int>> matrice = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
];
// Accedere a un elemento: riga 1, colonna 2 (indice da 0)
print(matrice[1][2]); // 6
// Modificare un elemento
matrice[0][0] = 10;
// Stampare tutta la matrice
for (var riga in matrice) {
print(riga);
}
}
VI esempio casting
Di fatto come in Java ma anche in Python ogni input è considerato string, successivamente con l’operazione di casting si arriva a definire il tipo di dato:
// Definizione della funzione
void saluta(String nome) {
print('Ciao, $nome!');
}
void main() {
// Chiamata della funzione
saluta('Francesco');
}
void main() {
String numeroStringa = "123";
int numeroIntero = int.parse(numeroStringa);
print(numeroIntero); // 123
print(numeroIntero.runtimeType); // int
}
void main() {
// Numero decimale (con la virgola)
double numeroDecimale = 3.14159;
print('Numero decimale: $numeroDecimale');
// Numero esponenziale (notazione scientifica)
double numeroEsponenziale = 1.23e4; // equivalente a 1.23 * 10^4 = 12300
print('Numero esponenziale: $numeroEsponenziale');
// Altro esempio di $esponenziale negativo
double piccoloNumero = 5.67e-3; // 5.67 * 10^-3 = 0.00567
print('Piccolo numero: piccoloNumero');
}
Come ultimo passo si noti il concetto di funzione.
// Definizione della funzione
void saluta(String nome) {
print('Ciao, $nome!');
}
void main() {
// Chiamata della funzione
saluta('Francesco');
}
Per chi è abituato a programmi compilati si nota che la definizione di funzione si ha prima del main() se si usa la piattaforma on line.
Ecco un altro esempio di funzione da cui poi definisco i vari tipi di funzione:
int somma(int a,int b) {
int c;
c= a + b;
return (c);
}
void main() {
int x = 3;
int y = 4;
int z = somma(x,y);
print("La somma risulta $z");
}
si possono definire anche le funzioni dopo il main() quando si usa dart all’interno del Visual Studio Code esattamente come le funzioni prototipo in C++.
L’uso di $z solo quando vi è una stringa al cui si mette la variabile con il numero.
I tipi di dato in dart sono i seguenti:
int, double, num che contiene dia gli int che i double, string e bool
Tipi complessi:
list, set, map.
Esempi di variabile globale:
// Variabile globale
int counter = 0;
void increment() {
counter++;
}
void main() {
print(counter); // 0
increment();
print(counter); // 1
}
Lo scopo di questo post è mostrare subito la potenzialità di un ambiente di sviluppo on line.
Prerequisiti è conoscere SQL, conoscere PHP e naturalmente conoscere il linguaggio DART nel framework FLUTTER.
Lo scopo è mostrare un’applicazione completa per poi scendere nei particolari nei post successivi.
L’ambiente di sviluppo on line è infinity free.net
Esso consente di non installare un ambiente XAMP (Linux, Apache, MySQL, PHP) sul proprio host ma utilizzare un server on line, naturalmente con tutte le limitazioni del caso.
Dopo essersi loggato si crea un ambiente gratuito con un URL fornito dalla piattaforma e naturalmente non commerciale.
Nel mio caso, ad oggi, data di scrittura del post, accedo con https//bragadin.42web.io
Il PHP come eventualmente le mie pagine web vengono inserite nella cartella htdocs.
L’account viene assegnato casualmente ad esempio il nome del database è if0_39612443_francesco202
Codice SQL per la creazione della tabella.
CREATE TABLE utenti ( id INT PRIMARY KEY AUTO_INCREMENT, nome VARCHAR(100) );
una chiave primaria che si auto incrementa ed un campo di tipo testo.
Quindi inserisco tre record:
INSERT INTO nome_tabella (colonna1, colonna2, colonna3)
VALUES ('valore1', 'valore2', valore3);
dove a valore1, valore2 e valore3 ho inserito tre nomi.
Adesso scrivo nella libreria il file htdocs il file in PHP get_anagrafica.php
<?php
// Connessione al database
$host = 'sql100.infinityfree.com';
$dbname = 'if0_39612443_francesco2025';
$username = 'xxxxxxxx';
$password = 'xxxxxxxx';
$conn = new mysqli($host, $username, $password, $dbname);
// Controllo connessione
if ($conn->connect_error) {
die("Connessione fallita: " . $conn->connect_error);
}
// Query per ottenere gli ultimi 3 record
$sql = "SELECT * FROM anagrafica ORDER BY id DESC LIMIT 3";
$result = $conn->query($sql);
// Preparazione dell'array di risposta
$data = array();
if ($result->num_rows > 0) {
while($row = $result->fetch_assoc()) {
$data[] = $row;
}
}
// Restituisce i dati in formato JSON
header('Content-Type: application/json');
echo json_encode($data);
// Chiude la connessione
$conn->close();
?>
Digitando su un browser:
https://bragadin.42web.io/get_anagrafica.php
vedrei i tre record emessi in formato JSON che devono essere dati a flutter.
Con flutter la correzione del codice avviene in termini reali consentendo di diminuire i tempi di sviluppo.
VS Code se si vuole provare in locale altrimenti si può usare la piattaforma zapp.run
Editare il file pubsec.yaml sostituendo il codice esistente con il seguente:
name: anagrafica_app
description: Un'app Flutter per la gestione dell'anagrafica
publish_to: 'none' # Non pubblicare su pub.dev
version: 1.0.0+1
environment:
sdk: '>=3.3.0 <4.0.0'
dependencies:
flutter:
sdk: flutter
http: ^0.13.6
# Aggiungi altre dipendenze qui, se necessario
dev_dependencies:
flutter_test:
sdk: flutter
flutter_lints: ^3.0.1
flutter:
uses-material-design: true
è sufficiente invece che copiarlo tutto in zapp.run editare http: ^0.13.6 bisogna stare attenti all’esitazione perché il file di parametri è posizionale.
Dopo averlo modificato si deve andare in alto a destra è cliccare su pub get che permette il caricamento dei nuovi parametri. Non si può copiare il file così com’è perché la versione di flutter messa a disposizione dalla piattaforma on line non è perfettamente aggiornata.
andare quindi a editare il file main.dart con il seguente codice:
import 'package:flutter/material.dart';
import 'package:http/http.dart' as http;
import 'dart:convert';
void main() {
runApp(MyApp());
}
class MyApp extends StatelessWidget {
@override
Widget build(BuildContext context) {
return MaterialApp(
title: 'Anagrafica',
home: AnagraficaPage(),
);
}
}
class AnagraficaPage extends StatefulWidget {
@override
_AnagraficaPageState createState() => _AnagraficaPageState();
}
class _AnagraficaPageState extends State<AnagraficaPage> {
List<dynamic> nomi = [];
Future<void> fetchData() async {
final response = await http.get(Uri.parse(
'https://bragadin.42web.io/get_anagrafica.php')); // <-- Modifica con il tuo URL PHP
if (response.statusCode == 200) {
setState(() {
nomi = json.decode(response.body);
});
} else {
throw Exception('Errore nel caricamento dei dati');
}
}
@override
void initState() {
super.initState();
fetchData();
}
@override
Widget build(BuildContext context) {
return Scaffold(
appBar: AppBar(
title: Text('Lista Anagrafica'),
),
body: nomi.isEmpty
? Center(child: CircularProgressIndicator())
: ListView.builder(
itemCount: nomi.length,
itemBuilder: (context, index) {
return ListTile(
title: Text(nomi[index]['nome']),
subtitle: Text('ID: ${nomi[index]['id']}'),
);
},
),
);
}
}
Su zapp.run dà un errore sempre a causa della versione, si deve andare a modificare il file widge_test.dart presente nella cartella test e togliere const alla riga 16. La cosa interessante, rispetto ad una programmazione tradizionale è il fatto che il codice viene controllato in tempo reale per cui l’errore viene evidenziato con una sottolineatura a zig Zag.
Adesso compare un altro errore causato dal fatto che zapp.run passa per il browser prima di fare la chiamata al server infinity in cui vi è il PHP. Tale errore non compare quando si va a creare l’app nativa perché non si passa per il browser.
Si deve modificare il codice PHP inserendo la tecnica di sicurezza CORS (Cross Origin Ressource Sharing); esso permette o blocca richieste http da un sito web verso un altro dominio diverso da quello da cui la pagina è stata caricata.
Pur avendo inserito la tecnica CORS con il browser Chrome continua a non funzionare allor a si prova con il browser Edge.
Questo codice flutter chiama il protocollo http che è un’opportuna libreria, se, per motivi di connessione non si vuole aspettare l’esito si può modificare il codice precedentemente nella seguente maniera:
import 'package:flutter/material.dart';
import 'dart:convert';
void main() {
runApp(MyApp());
}
class MyApp extends StatelessWidget {
@override
Widget build(BuildContext context) {
return MaterialApp(
title: 'Anagrafica',
home: AnagraficaPage(),
);
}
}
class AnagraficaPage extends StatefulWidget {
@override
_AnagraficaPageState createState() => _AnagraficaPageState();
}
class _AnagraficaPageState extends State<AnagraficaPage> {
List<dynamic> nomi = [];
Future<void> fetchData() async {
await Future.delayed(Duration(seconds: 2)); // Simula ritardo rete
final fakeResponse = jsonEncode([
{'id': 1, 'nome': 'Mario Rossi'},
{'id': 2, 'nome': 'Luigi Bianchi'},
{'id': 3, 'nome': 'Giulia Verdi'},
]);
setState(() {
nomi = json.decode(fakeResponse);
});
}
@override
void initState() {
super.initState();
fetchData();
}
@override
Widget build(BuildContext context) {
return Scaffold(
appBar: AppBar(
title: Text('Lista Anagrafica'),
),
body: nomi.isEmpty
? Center(child: CircularProgressIndicator())
: ListView.builder(
itemCount: nomi.length,
itemBuilder: (context, index) {
return ListTile(
title: Text(nomi[index]['nome']),
subtitle: Text('ID: ${nomi[index]['id']}'),
);
},
),
);
}
}
L’app avrà il seguente aspetto:
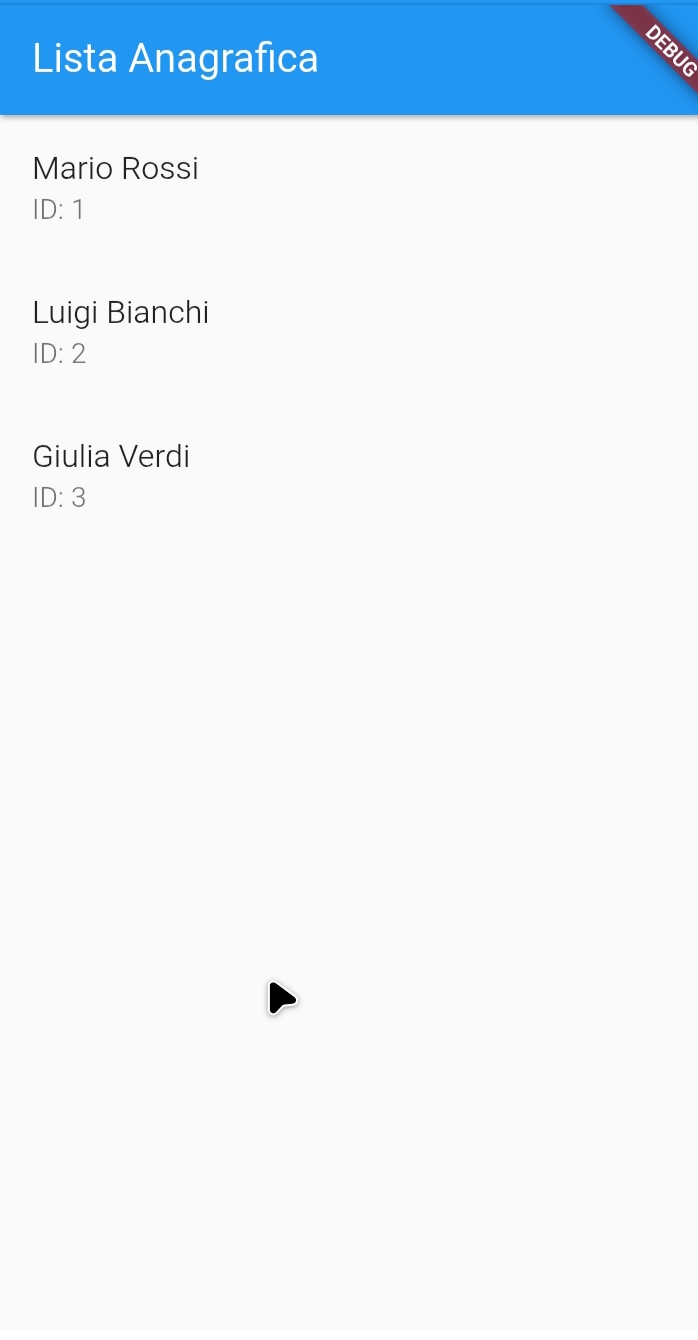
La conclusione è la seguente:
“L’ambiente di esecuzione di zapp.run consente lo sviluppo ed il test di app locali, ma limita le chiamate HTTPS dirette verso servizi esterni, richiedendo un backend o un proxy per l’accesso a risorse remote.”
Lo strumento che andrò a dettagliare nasce per lo sviluppo di app utilizzando il linguaggio Dart ed un uso massiccio di widget.
Per chi fosse poco avvezzo al concetto di widget si pensi ad un concetto di classe e suo ereditarietà e riscrittura dei relativi metodi.
In letteratura vi sono ormai numerosi esempi di scrittura con flutter e la stessa intelligenza artificiale aiuta moltissimo a scrivere il relativo codice ed anche a correggerlo.
A questo punto il mio scopo è usare l’intelligenza artificiale, dando una linea guida affinchè si possa realmente scrivere un’app utile per la quotidianità come ad esempio un accesso ad un archivio con la visualizzazione dei relativi record.
Cosa serve per scrivere un’app:
Un computer con almeno 8GB di RAM, meglio 16GB considerando comunque che a fronte di un codice molto “leggero” da fare eseguire sui cellulari richiede un alto consumo della CPU del “generatore” di codice.
Dart nasce prima di flutter nel 2011 con l’intento di sostituire JavaScript. Tutto il codice utilizzato dal Framework Flutter è scritto in Dart.
Dart letteralmente significa dardo quindi veloce, preciso e leggero nell’ottica dell’installazione su dispositivi mobili.
Flutter significa leggero considerando la possibilità di ricaricare il codice in tempo reale; questa è una caratteristica che potrebbe fare assomigliare il tutto ad un linguaggio interpretato.
Riflessione personale: provenendo da una cultura di programmazione in Fortran (due cicli di compilazione) quindi Cobol, C, C++, Phyton, per approdare in Java considero tale passo veramente molto importante ossia la possibilità di vedere le modifiche al codice in tempo reale.
Un altro aspetto che potrebbe fare vacillare il mondo Java e quello che si comincia ad essere scollegati dalla JVM ora in mano ad Oracle per approdare ad un eseguibile pronto ad essere installato sul proprio dispositivo mobile.
Un ultimo aspetto prima di tornare a parlare di dettagli tecnici: l’uso dei PC portatili, a mio avviso va verso il suo abbandono cominciando ad usare sempre più il proprio cellulare con una sua espansione verso un video più grande e lasciando il PC solo nell’ambito dello sviluppo.
Faccio la lista della spesa:
Android Studio è necessario per usare l’emulatore ANDROID e per usare ANDROID SDK (Software Development Kit). Sarà Android Studio che compilerà e creerà il file eseguibile da mettere sul dispositivo mobile (.apk).
Visual Studio Core e Android Studio sono due programmi che non comunicano tra loro. VS Core ha bisogno di programmi che vengono installati attraverso il pacchetto di Android Studio.
Facendo una metafora VS Core è una barca che ha bisogno dell’acqua per poter essere usata. Android Studio fa da diga che blocca l’acqua creando un lago con l’acqua di cui la barca ha bisogno.
Nel prossimo post illustrò come sono riuscito a creare un’intera struttura flutter solo con i materiali messi a disposizione gratuitamente da varie piattaforme on line.

Insegnare la crittografia nell’indirizzo R.I.M. (Relazioni Internazionali per il Marketing) ha molto senso, soprattutto considerando l’importanza crescente della sicurezza dei dati e della comunicazione digitale nel mondo degli affari internazionali e del marketing.
Ecco alcuni motivi chiave:
Nel marketing internazionale, le aziende gestiscono una grande quantità di dati sensibili, come informazioni sui clienti, strategie di mercato e dati finanziari. La crittografia aiuta a proteggere queste informazioni da accessi non autorizzati.
Quando si lavora con partner internazionali, spesso si utilizzano canali digitali per comunicare. L’uso della crittografia end-to-end garantisce che le comunicazioni, incluse e-mail e videochiamate, siano protette.
Con regolamenti come il GDPR (General Data Protection Regulation) in Europa, le aziende devono garantire la protezione dei dati personali. La crittografia è una delle misure principali per rispettare queste normative.
Un’azienda che protegge adeguatamente i dati dei propri clienti attraverso la crittografia aumenta la propria reputazione e la fiducia del mercato.
Nel marketing, le transazioni online sono fondamentali. La crittografia garantisce che i pagamenti e i dati delle carte di credito siano protetti.
L’indirizzo R.I.M. prepara gli studenti a lavorare in contesti internazionali, dove la protezione delle informazioni durante il trasferimento di dati tra paesi è cruciale.
Imparare la crittografia sviluppa competenze tecniche che possono ampliare le opportunità professionali degli studenti, rendendoli più competitivi nel mercato del lavoro.

Se si vogliono usare le tabelle i comandi base sono i seguenti:
ogni singolo tag deve poi essere opportunamente chiuso </table>, </tr>,</td>
Gli attributi al tag table sono:
Gli attributi del tag tr sono:
align: specifica l’allineamento del contenuto (left, center, right)bgcolor: definisce il colore di sfondo della rigavalign: specifica l’allineamento verticale (top, middle, bottom)Gli attributo del tag td:
colspan: specifica il numero di colonne che la cella deve occupare.rowspan: specifica il numero di righe che la cella deve occupare.align:allinea il contenuto (left, center, right, justify).valign: specifica l’allineamento verticale (top, middle, bottom).bgcolor:definisce il colore di sfondo della cella.width:definisce la larghezza della cella.height:definisce l’altezza della cella.Ad esempio si può scrivere il seguente codice essenziale
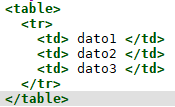
Per avere il risultato dell’immagine precedente si usa l’attributo colspan=4 nel tag <th> e l’attributo rowspan=2 nel tab td.
Ultima nota per usare l’intestazione della tabella si usa il tag <th> con il relativo tag di chiusura </th>