[:it]

samy charnine
Semplificare le seguenti espressioni:
la difficoltà di questi prodotti è nel cercare di ricordare le seguenti due proprietà delle potenze:
- lo sviluppo del prodotto è sommare gli esponenti
- lo sviluppo dell’elevazione alla potenza è il prodotto degli esponenti.
- Al termine bisogna sommare i termini SIMILI ossia quelli con la parte letterale uguale.
- Se si ricorda poi che
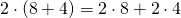 ossia moltiplico per due prima l’8 e poi il 4, si riesce a sviluppare il prodotto tra monomi e polinomi.
ossia moltiplico per due prima l’8 e poi il 4, si riesce a sviluppare il prodotto tra monomi e polinomi.
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
|
| 6.5. |
|
| 6.6. |
|
| 6.7. |
|
| 6.8. |
|
| 6.9. |
|
| 6.10. |
|
| 6.11. |
|
| 6.12. |
|
| 6.13. |
|
| 6.14. |
|
| 6.15. |
|
| 6.16. |
|
| 6.17. |
|
| 6.18. |
|
| 6.19. |
|
| 6.20. |
|
6.21. 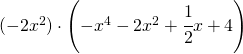 |
|
6.22. 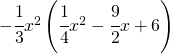 |
[:en]Semplificare le seguenti espressioni:
[tra le parentesi quadre vi sono le soluzioni]
La difficoltà di questi prodotti è nel cercare di ricordare le seguenti due proprietà delle potenze:
- lo sviluppo del prodotto è sommare gli esponenti
- lo sviluppo dell’elevazione alla potenza è il prodotto degli esponenti.
- Al termine bisogna sommare i termini SIMILI ossia quelli con la parte letterale uguale.
- Se si ricorda poi che
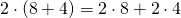 ossia moltiplico per due prima l’8 e poi il 4, si riesce a sviluppare il prodotto tra monomi e polinomi.
ossia moltiplico per due prima l’8 e poi il 4, si riesce a sviluppare il prodotto tra monomi e polinomi.
1) ![]() Ris
Ris ![]()
2) ![]() Ris
Ris ![]()
3) ![]() Ris
Ris ![]()
4) ![]() Ris
Ris ![]()
5) ![]() Ris
Ris ![]()
6) ![]() Ris
Ris ![]()
7) ![]() Ris
Ris ![]()
8) ![]() Ris
Ris ![]()
9) ![]() Ris
Ris ![]()
10) ![]() Ris
Ris ![]()
11) ![]() Ris
Ris ![]()
12) ![]() Ris
Ris ![]()
13) ![]() Ris
Ris ![]()
14) ![]()
![]()
15) ![]() Ris
Ris ![]()
16) ![]() Ris
Ris ![]()
17) ![]() Ris
Ris ![]()
18) ![]() Ris
Ris ![]()
19) ![]() Ris
Ris ![]()
20) ![]() Ris
Ris ![]()
21) 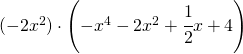 Ris
Ris ![]()
22) 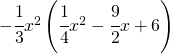 Ris
Ris ![]() [:de]Semplificare le seguenti espressioni:
[:de]Semplificare le seguenti espressioni:
[tra le parentesi quadre vi sono le soluzioni]
La difficoltà di questi prodotti è nel cercare di ricordare le seguenti due proprietà delle potenze:
- lo sviluppo del prodotto è sommare gli esponenti
- lo sviluppo dell’elevazione alla potenza è il prodotto degli esponenti.
- Al termine bisogna sommare i termini SIMILI ossia quelli con la parte letterale uguale.
- Se si ricorda poi che
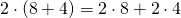 ossia moltiplico per due prima l’8 e poi il 4, si riesce a sviluppare il prodotto tra monomi e polinomi.
ossia moltiplico per due prima l’8 e poi il 4, si riesce a sviluppare il prodotto tra monomi e polinomi.
1) ![]() Ris
Ris ![]()
2) ![]() Ris
Ris ![]()
3) ![]() Ris
Ris ![]()
4) ![]() Ris
Ris ![]()
5) ![]() Ris
Ris ![]()
6) ![]() Ris
Ris ![]()
7) ![]() Ris
Ris ![]()
8) ![]() Ris
Ris ![]()
9) ![]() Ris
Ris ![]()
10) ![]() Ris
Ris ![]()
11) ![]() Ris
Ris ![]()
12) ![]() Ris
Ris ![]()
13) ![]() Ris
Ris ![]()
14) ![]()
![]()
15) ![]() Ris
Ris ![]()
16) ![]() Ris
Ris ![]()
17) ![]() Ris
Ris ![]()
18) ![]() Ris
Ris ![]()
19) ![]() Ris
Ris ![]()
20) ![]() Ris
Ris ![]()
21) 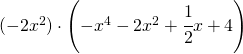 Ris
Ris ![]()
22) 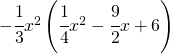 Ris
Ris ![]() [:]
[:]
