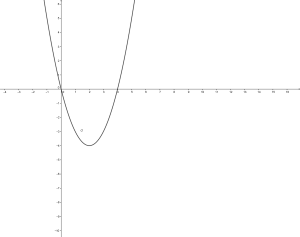
Per parabola spuria considero di questo tipo:
![]()
1 passo: intersezioni con gli assi
pongo
![]()
ed ho:
![]()
pongo
![]()
![]()
questa volta non serve usare la formula risolutiva per l’equazione di secondo grado ma è sufficiente raccogliere la x ossia:
![]()
la prima parte conferma la soluzione già trovata precedentemente ossia
x=0
la seconda è la soluzione dell’equazione di primo grado:
![]()
ossia
![]()
passo2: analisi del coefficiente A per capire la concavità
A=1
per cui la concavità è verso l’alto.
Il grafico risulta quindi:
passo3: calcolo delle coordinate del vertice
A=1; B=-4; C=0
![]()
![]()