[:it]

Jacek Yerka
La circonferenza è quel luogo del piano descritto da tutti quei punti equidistanti da un punto C chiamato centro.
Si forniscono normalmente queste due equazioni che sono equivalenti ma applicabili in ambiti diversi a seconda dei dati che si forniscono o di cosa si deve trovare.
Prima forma
![]()
in questo caso le coordinate del centro in funzione di a e b sono:
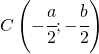
ed il raggio è:
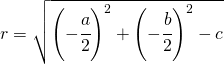
Seconda forma
![]()
le cui coordinate del centro sono:
![]()
ed il raggio è appunto
![]()
[:en]

Jacek Yerka
La circonferenza è quel luogo del piano descritto da tutti quei punti equidistanti da un punto C chiamato centro.
Si forniscono normalmente queste due equazioni che sono equivalenti ma applicabili in ambiti diversi a seconda dei dati che si forniscono o di cosa si deve trovare.
Prima forma
![]()
in questo caso le coordinate del centro in funzione di a e b sono:
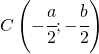
ed il raggio è:
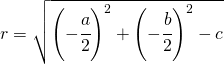
Seconda forma
![]()
le cui coordinate del centro sono:
![]()
ed il raggio è appunto
![]()
[:de]

Jacek Jerka
Der Umfang ist der Ort der Ebene, der von all diesen Punkten von einem Punkt gleich weit entfernt ist und C genannt wird.
In der Regel werden diese beiden Gleichungen geliefert, die gleichwertig sind, aber in verschiedenen Bereichen in Abhängigkeit der angegebenen Daten anwendbar sind oder von dem, was gesucht wird, abhängig sind.
Erste Form
![]()
In diesem Fall sind die Koordinaten der Mitte in Funktion von a und b folgende :
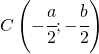
und der Radius ist :
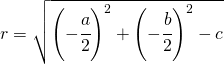
Zweite Form
![]()
Die Koordinaten der Mitte sind:
![]()
und der Radius ist demzufolge
![]() [:]
[:]
