Metodo di Cramer: applicazione ai sistemi 2×2

Pubblicato il 10 Febbraio 2016 da admin

th1NG1F1DU Il metodo di Cramer lo applico al seguente sistema:

$\left\{\begin{matrix} 2\cdot x+3\cdot y=4\\ 5\cdot x+6\cdot y=7 \end{matrix}\right.$

Si notino le seguenti cose:

ho incolonnato il sistema ossia prima le x poi le y ed a destra dell’uguale il termine noto.
ogni volta che voglio applicare il metodo di Cramer devo ordinare il sistema.

Per trovare il valore della x:

$x=\cfrac{\begin{vmatrix} 4 &3 \\ 7 &6 \end{vmatrix}}{\begin{vmatrix} 2 &3 \\ 5 &6 \end{vmatrix}}=\cfrac{24-21}{12-15}=\cfrac{3}{-3}=-1$

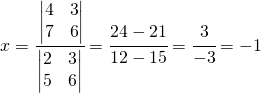
Per trovare il valore della y:

$y=\cfrac{\begin{vmatrix} 2 &4 \\ 5 &7 \end{vmatrix}}{\begin{vmatrix} 2 &3 \\ 5 &6 \end{vmatrix}}=\cfrac{14-20}{12-15}=\cfrac{-6}{-3}=2$

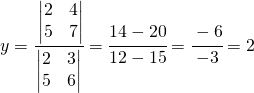
Spiegazione:

il denominatore è formato dai coefficienti che moltiplicano la x e la y.
per trovare la x si immagina di coprire la colonna delle x ed al suo posto inserire i termini noti o numeri a destra dell’uguale.
per trovare la y si immagini di coprire la colonna delle y ed al suo posto inserire i termini noti.
eseguire quindi il determinante delle matrici, si noti che il denominatore è uguale sia per la determinazione della x che della y.

Questa voce è stata pubblicata in Senza categoria. Contrassegna il permalink.

Lascia un commento Annulla risposta