Per  risolvere i sistemi di disequazione è sufficiente essere in grado di risolvere le disequazioni lineari e ricordarsi che la soluzione viene data dalla regione in cui entrambe contemporaneamente risolvono le rispettive disequazioni di partenza.
risolvere i sistemi di disequazione è sufficiente essere in grado di risolvere le disequazioni lineari e ricordarsi che la soluzione viene data dalla regione in cui entrambe contemporaneamente risolvono le rispettive disequazioni di partenza.
Per un livello minimo (6)
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
![Rendered by QuickLaTeX.com \left [ \cfrac{3}{2}\leq x\leq \cfrac{10}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d874d6865e9738e5a0e0a8e1ee9670d1_l3.png) |
| 6.5. |
![Rendered by QuickLaTeX.com \left [ x<\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5fe59560429192c0c5955eed241d455b_l3.png) |
| 6.6. |
![Rendered by QuickLaTeX.com \left [ \cfrac{5}{2}\leq x<\cfrac{7}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-cc102b92e782701a3973533343d93ee5_l3.png) |
| 6.7. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{8}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e63eca605efe9170d16822b5d0d2adf2_l3.png) |
| 6.8. |
![Rendered by QuickLaTeX.com \left [ x<-\cfrac{1}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5a3e5d51b7e2a1b42cdda69308d34417_l3.png) |
| 6.9. |
![Rendered by QuickLaTeX.com \left [ -\cfrac{4}{3}<x<\cfrac{5}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-72e747f7aabf492ce7c0ef9261028634_l3.png) |
Per un livello discreto (7)
7.1. 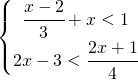 |
![Rendered by QuickLaTeX.com \left [ x<\cfrac{5}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-96dbd5e87d5edb2f6469946aaa0fb7dc_l3.png) |
7.2. 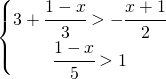 |
|
7.3. 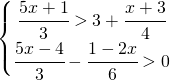 |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{41}{17}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e549ca2ccebdcab7ea6766e9bb3a5cec_l3.png) |
Per un buon livello (8)
8.1. 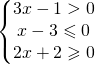 . . |
![Rendered by QuickLaTeX.com \left [ \cfrac{1}{3}<x\leqslant 3 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-aee70d4e862ad2e7591477f51a8e5b60_l3.png) |
8.2. 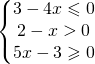 |
![Rendered by QuickLaTeX.com \left [ \cfrac{3}{4}\leqslant x<2 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-be87c42e4e2f223068cd48943fa66bbe_l3.png) |
8.3. 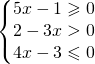 |
![Rendered by QuickLaTeX.com \left [ \cfrac{1}{5}\leqslant x< \cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d7a4db19a611fb5dcfefdafcdf341945_l3.png) |
8.4. 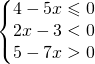 |
|
8.5. 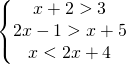 |
|
8.6. 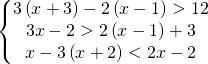 |
Verso un ottimo livello (9/10)
9.1. 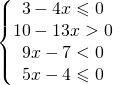 |
![Rendered by QuickLaTeX.com \left [ \cfrac{3}{4}\leqslant x<\frac{10}{13} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-79634375285228736576b033de4b9385_l3.png) |
9.2. 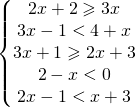 |

cosa sarebbe il 6.4?
Ho inserito le soluzioni prova a capire se è chiaro grazie:
https://www.whymatematica.com/?p=4417