[:it]

Jim Warren
La parabola è il luogo geometrico dei punti del piano equidistanti da un punto, detto fuoco, e da una retta detta direttrice.
Tale definizione mette in evidenza che le quattro cose che caratterizzano una parabola sono:
- il vertice
- l’asse di simmetria
- il fuoco
- la direttrice
L’equazione generica della parabola risulta:
![]()
dove a,b, c sono dei valori qualsiasi.
Si noti che la ![]() altrimenti la parabola degenera in una retta.
altrimenti la parabola degenera in una retta.
I parametri precedenti si esprimono in funzione dei parametri a,b,c.
Vertice 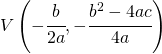
Asse di simmetria ![]()
Fuoco 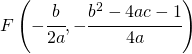
Direttrice ![]()
Come esempio si studi la seguente parabola:
![]()
in questo caso
a=1
b=-5
c=6
Tutti i quattro parametri si ricavano calcolando:
![]()
![]()
Vertice 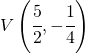
Asse di simmetria ![]()
Fuoco 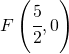
Direttrice ![]()
Graficamente risulta

[:en]

Jim Warren
La parabola è il luogo geometrico dei punti del piano equidistanti da un punto, detto fuoco, e da una retta detta direttrice.
Tale definizione mette in evidenza che le quattro cose che caratterizzano una parabola sono:
- il vertice
- l’asse di simmetria
- il fuoco
- la direttrice
L’equazione generica della parabola risulta:
![]()
dove a,b, c sono dei valori qualsiasi.
Si noti che la ![]() altrimenti la parabola degenera in una retta.
altrimenti la parabola degenera in una retta.
I parametri precedenti si esprimono in funzione dei parametri a,b,c.
Vertice 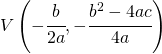
Asse di simmetria ![]()
Fuoco 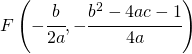
Direttrice ![]()
Come esempio si studi la seguente parabola:
![]()
in questo caso
a=1
b=-5
c=6
Tutti i quattro parametri si ricavano calcolando:
![]()
![]()
Vertice 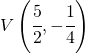
Asse di simmetria ![]()
Fuoco 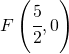
Direttrice ![]()
Graficamente risulta

Versione tedesca[:de]

Shana and Robert Parke Harrison
Shana and Robert Parke HarrisonDie Parabel ist ein Teil des Koordinatensystemes, in dem mehere Punkte immer den gleichen Abstand halten( der so gennante “Brennpunkt”) und einer Geraden (die sogennante Leitlinie).
Diese Definition beweist also die 4 Grundzüge der Parabel:
1.Der Scheitelpunkt
2.Die Symmetrieachse
3.Der Brennpunkt
4.Die Leitlinie
Die generelle Gleichung der Parabel wäre:
![]()
Wo Punkt A,B und C verschiedene Ziffern haben können.
Man sieht, dass ![]() Weil sonst wäre die Parabel eine Gerade.
Weil sonst wäre die Parabel eine Gerade.
Die vorherigen Parameter sprechen in Funktion als Parameter von A,B und C.
Scheitelpunkt 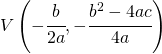
Symmetrieachse ![]()
Brennpunkt 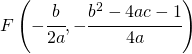
Leitlinie ![]()
Als Beispiel hat man hier die folgende Parabel:
![]()
In diesem Fall
a=1
b=-5
c=6
Alle vier Parameter erhält man aus der Rechnung:
![]()
![]()
Scheitelpunkt 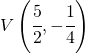
Symmetrieachse ![]()
Brennpunkt 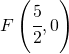
Leitlinie ![]()
Diese ist die grafische Darstellung:
 [:]
[:]
