[:it]Soluzioni esercizi sull’ellisse[:]

Pubblicato il 8 Aprile 2016 da admin

[:it]6.1

L’equazione generica dell’ellisse è:

$\cfrac{x^{2}}{a^{2}}+\cfrac{y^{2}}{b^{2}}=1$

e confrontandola con quella dell’esercizio

$\cfrac{x^{2}}{4}}+\cfrac{y^{2}}{1}=1$

si nota immediatamente che

$a^{2}=4$

$b^{2}=1$

ed ho quindi trovato i vertici dell’ellisse che sono i punti in cui l’ellisse interseca l’asse delle ascisse e l’asse delle ordinate.

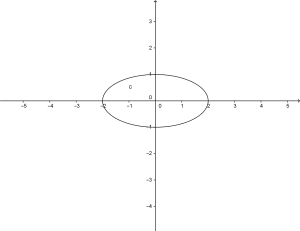
+a e -a sono le intersezioni con l’asse delle ascisse

+b e -b sono le intersezioni con l’asse delle ordinate

per trovare qual è l’asse maggiore si confrontano i punti a e b e si nota che a che vale 2 è maggiore di b che vale 1.

Per trovare le coordinate dei fuochi si usa la seguente formula:

$c^{2}=a^{2}-b^{2}$

sostituendo alle lettere i rispettivi valori si ha:

$c=\sqrt{4-1}=\sqrt{3}$

determinata la c posso trovare l’eccentricità che mi fornisce di quanto la mia ellisse sia “schiacciata”

$e=\cfrac{c}{a}=\cfrac{\sqrt{3}}{2}$

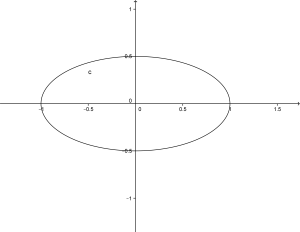
Adesso posso disegnare l’ellisse il cui grafico risulta:

ellisse

7.1.

Confronto

$x^2+4y^2=1$

con la forma canonica

$\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1$

noto subito che nell’esercizio devo manipolare il coefficiente che moltiplica $y^2$ in questa maniera:

$\cfrac{x^2}{1}+\cfrac{y^2}{\frac{1}{4}}=1$

così posso subito identificare:

$a^2=1$

e

$b^2=\cfrac{1}{4}$

quindi $a=\sqrt{1}=1$ e $b=\sqrt{\cfrac{1}{4}}=\cfrac{1}{2}$

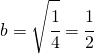
Le coordinate dei fuochi

$c=\sqrt{1-\frac{1}{4}}=\sqrt{\cfrac{3}{4}}$

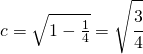
ed infine l’eccentricità

$e=\sqrt{\cfrac{3}{4}}$

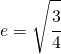
il grafico di questa ellisse risulta:

ellisse4

8.1.

Confronto

$4x^2+9y^2=25$

con l’equazione canonica

$\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1$

mi devo trovar l’uno, per cui diviso a sinistra e a destra per 25 e quindi l’equazione di partenza risulta.

[:]

Questa voce è stata pubblicata in Senza categoria. Contrassegna il permalink.

Lascia un commento Annulla risposta