[:it]
George Grie
La proprietà invariantiva delle frazioni è alla base di una delle più potenti proprietà per poterle manipolare, facendone la somma, la moltiplicazione, la semplificazione: in partica manipolare le frazioni in maniera esattamente uguale a dei numeri interi.
PROPRIETA’ INVARIANTIVA
Moltiplicando il numeratore ed il denominatore per uno stesso numero si ha una frazione equivalente.
Dividendo il numeratore ed il denominatore per uno stesso numero si ha una frazione equivalente.
Due frazioni si dicono equivalenti quando rappresentano lo stesso valore ad esempio 
è uguale a 
.
La conseguenza fondamentale di tale proprietà è la semplificazione di una frazione:
oppure il confronto tra frazioni:
devo capire quale tra le seguenti due frazioni è la più grande.
e 
- calcolare il m.c.m. tra i denominatori –> m.c.m.{5,6}=30
- Divido il m.c.m. appena trovato per il primo denominatore
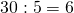
- Moltiplico il numeratore ed il denominatore della prima frazione per
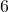ossia:
- Divido il m.c.m. appena trovato per il secondo denominatore
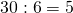
- Moltiplico il numeratore ed il denominatore della seconda frazione per
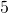ossia:
Adesso le due frazioni iniziali sono diventate:
e 
e confrontando solo il numeratore osservo che:
per cui si può dire che:
.
E’ più facile farlo che descriverlo![:]
weee
Olaaaaa