[:it]
Trovare una soluzione non significa che si debba conoscere esattamente il suo valore preciso ma è sufficiente uno approssimato.
Il procedimento si basa sul punto medio di un intervallo, in cui si presuppone esserci una soluzione. La scelta dell’intervallo deve soddisfare il teorema dell’unicità del limite.
Il punto medio si calcola come:
Il valore del punto medio meno la soluzione precisa (che non si conosce) è sicuramente minore di metà dell’intervallo stesso.
Ossia in maniera algebrica:
Quindi si prende metà dell’intervallo, che invece si conosce, come stima dell’approssimazione. Questa scelta assolutamente corretta ha come svantaggio il fatto che, per arrivare all’approssimazione voluta, bisogna reiterare il procedimento numerose volte.
L’approssimazione viene definita come:
Il procedimento si itera prendendo come nuovo estremo dell’intervallo il punto medio trovato e si calcola quindi la nuova media e la nuova stima finchè essa sia minore di quella voluta.
Nei dettagli:
Data l’equazione 
, si cerchi un intervallo ![\left [ a_{0};b_{0} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-c4f60d428c07f96a626774d8b1999435_l3.png "Rendered by QuickLaTeX.com")
tale che 
.
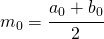- determinare il punto medio dell’intervallo , , e si calcoli
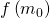. - se
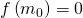, allora 
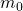è proprio la soluzione e si termina il ciclo altrimenti si va al passo successivo. - se
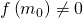allora 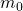è un valore approssimato della soluzione e si calcola 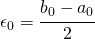. - Se
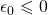di quella voluta si esce da ciclo altrimenti si va al passo successivo - Si sceglie il nuovo intervallo in questa maniera:
se 
allora 
, 
se 
allora 
, 
6. si torna torna al numero 1 con in nuovi intervalli.
[:]