[:it]
Quando unisco due punti creo un segmento, se questo viene prolungato ai suoi estremi creo una retta.
Una retta nello spazio, lasciata senza alcun riferimento, serve a poco per cui viene sempre disegnata sul piano cartesiano che mette in relazione una cosa in funzione di un’altra:
- il numero di vendite in funzione dei giorni
- gli ingredienti di una torta in funzione del tipo di torta
- il numero di passeggeri in funzione del costo del biglietto
- il numero di studenti in funzione della scuola di provenienza
- le promozioni in funzione della classe.
Una retta mette in relazione l’asse delle y con l’asse delle x.
In generale una retta viene scritta come:
(1) 
prende il nome di coefficiente angolare in quanto esso mi fornisce l’inclinazione della retta.
prende il nome di ordinata all’origine perché è il valore dell’intersezione della retta con l’asse delle ordinate.
Le rette hanno quindi sempre equazione
(2) 
ma comunemente si adotta la forma (1) perché fornisce molte più informazioni della forma (2).
Come faccio a rappresentare una retta sul piano cartesiano?
Fondamentale: sono sufficienti due punti per rappresentare una retta!
SOLO DUE ossia è sufficiente prendere un valore a caso di x ed uno di y oppure due di x o due di y, l’altra incognita si trova partendo dall’equazione della retta.
Ad esempio:
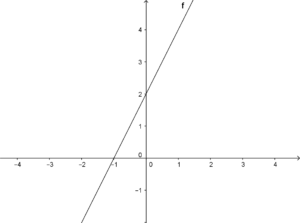
Metodo intersezione con gli assi anche illustrato nel video relativo
- prendo il valore
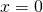troverò che 
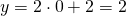ed ho trovato il punto A(0;2). - Poi prendo y=0 allora avrò
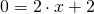ossia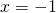 
per cui il secondo punto è B(-1;0).
Segno i due punti sul piano cartesiano, li unisco ed ho proprio la retta cercata
[:]