[:it] 9.1.
9.1. ![]()
Effettuo la seguente sostituzione:
(1) ![]()
![]()
elevo entrambi i membri alla seconda in maniera da non avere più la radice quadrata
![]()
![]()
![]()
![]()
facendo la derivata a desta e sinistra si ha:
![]()
(2) ![]()
![]()
(3) ![]()
Adesso sostituendo la (2) e la (3) nell’integrale di partenza si ha:
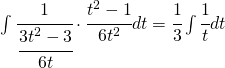
![]()
e sostituendo la (1) si ha come risultato:
![]() [:]
[:]
