[:it]

Samy Charnine
Somma
Se si vogliono sommare gli euro l’operazione che si effettua è:
5€ + 7€ =12€
in maniera analoga se si vogliono sommare le mele o le pere presenti in una cassetta della frutta le raggruppo per tipo e le sommo.
La regola generale afferma che:
La somma algebrica di due o più monomi simili è un monomio simile a quelli dati che ha per coefficiente la somma algebrica dei coefficienti, oppure è un monomio nullo se questa è uguale a 0.
L’operazione della somma di termini simili si chiama riduzione dei monomi simili
Esempio:
![]()
sommo SOLO i monomi simili
![]()
![]()
![]()
Moltiplicazione
Il prodotto di due o più monomi non nulli è un monomio che ha come coefficiente il prodotto dei coefficienti dei monomi dati e come parte letterale il prodotto delle parti letterali.
Se uno dei monomi è nullo, il prodotto è il monomio nullo.
Regola pratica
- prima il prodotto dei segni
- poi il prodotto dei coefficienti
- addizione degli esponenti delle lettere uguali
DA RICORDARSI SEMPRE:
![]()
![]()
Esempio:
![]()
Divisione
La divisione o quoziente tra due monomi, non nulli e divisibili, è un monomio che ha, come coefficiente, il quoziente dei coefficienti dei due monomi dati e, come parte letterale, quella formata da tutti i fattori letterali del dividendo, ciascuno elevato alla differenza degli esponenti che esso ha nel dividendo e nel divisore.
Regola pratica
- prodotto dei segni
- divisione tra i coefficienti (valgono le regole della divisione tra le frazioni)
- sottrazione degli esponenti delle lettere uguali
Esempio:
![]()
nel caso si abbiano delle frazioni:
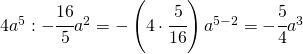 [:]
[:]
