[:it]Un piano nello spazio ha la seguente equazione:
![]()
i coefficienti a, b e c rappresentano le coordinate del vettore perpendicolare al piano.
Ad esempio la rappresentazione del piano ![]() ha come vettore
ha come vettore ![]() è un vettore che è perpendicolare la piano dato.
è un vettore che è perpendicolare la piano dato.
Graficamente si ha la seguente situazione:
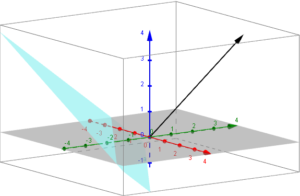
in cui in azzurro si nota il piano ed in grigio il vettore che è proporio perpendicolare al piano in esempio con le coordinate precedentemente date.
Tale affermazione è molto utile quando si devono studiare le posizioni reciproche tra un piano ed una retta.
PIANO PASSANTE PER TRE PUNTI
Un piano è sempre identificato da tre punti per cui, se fossero dati e si dovesse trovare il relativo piano che li contiene, è sufficente sostituire le loro coordinate nell’equazione generica del piano e risolvere il relativo sistema.
Vi è una particolarità: ci si troverà un sistema di tre equazioni in quattro incognite. Lo si risolve come se vi fossero tre incognite, la quarta verrà poi eliminata quando si andranno a sostituire i valori nel piano di partenza.
Ad esempio trovare l’equazione del piano passante per questi tre punti
A(1,1,0) B(0,-3,1) C(2,-2,0)
sostituendo le coordinate nell’equazione generica del piano ho:
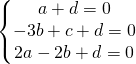
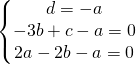
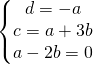
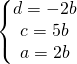
L’equazione del piano diventa:
![]()
Ora divido tutto per ![]() e l’equazione del piano diventa:
e l’equazione del piano diventa:
![]() .[:]
.[:]
