[:it]
Consideriamo la funzione ![]() , periodica di periodo
, periodica di periodo ![]() il cui grafico, nell’intervallo
il cui grafico, nell’intervallo ![]() , è il seguente:
, è il seguente:
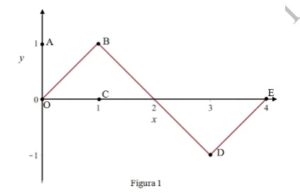
Come si evince dalla figura 1, i tratti OB, BD, DE del grafico sono i segmenti i cui estremi hanno coordinate: ![]() .
.
1) Stabilisci in quali punti del suo insieme di definizione la funzione ![]() è continua e in quali è derivabile e verifica l’esistenza dei limiti:
è continua e in quali è derivabile e verifica l’esistenza dei limiti: ![]() e
e ![]() ; qualora esistano, determinare il valore.
; qualora esistano, determinare il valore.
Rappresenta inoltre, per ![]() , i grafici delle funzioni:
, i grafici delle funzioni:
(1) ![]()
(2) ![]()
Prerequisiti
- conoscere le caratteristiche dei punti angolosi
- retta passante per due punti
- conoscere i limiti
- conoscere bene le derivate
- conoscere gli integrali
- saper fare un grafico con sicurezza delle funzioni elementari quali retta e parabola
Svolgimento
![]()
non può esistere essendo f(x) una funzione che oscilla tra +1 e -1.
Invece
![]()
in quanto f(x) varia sempre da +1 a -1 e diviso per un numero che tende all’infinito inevitabilmente si avrà lo 0 come risultato.
Per risolvere la (1), preferisco prima scrivere le equazioni che rappresentano la funzione periodica ![]() .
.
L’equazione della retta passante per ![]() è proprio la bisettrice del primo quadrante
è proprio la bisettrice del primo quadrante ![]() .
.
Per avere l’equazione della retta passante per ![]() uso la relazione:
uso la relazione:
(3) ![]()
(4) 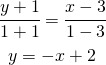
Per avere l’equazione della retta passante per ![]() uso la relazione (3)
uso la relazione (3)
(5) 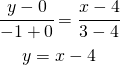
Ricapitolando:
(6) 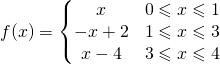
La (1) adesso si può calcolare derivando la (6) tra gli opportuni intervalli:
(7) 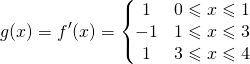
La sua rappresentazione grafica è:
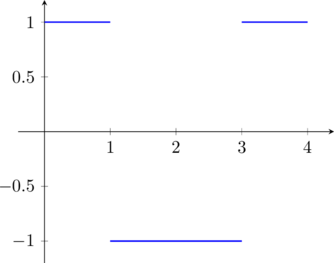
Per trovare la (2), uso ancora la (6) considerando gli intervalli opportuni.
Per ![]()
(8) ![]()
Per ![]()
(9) 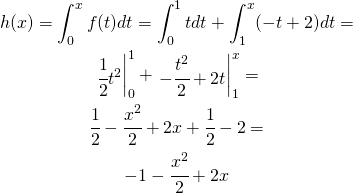
Per ![]()
(10) 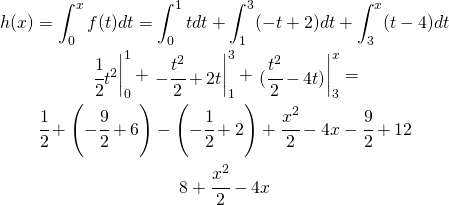
Riunisco la (8) la (9) e la (10)
(11) 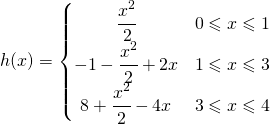
La sua rappresentazione grafica è la rappresentazione di tre parabole negli opportuni intervalli:
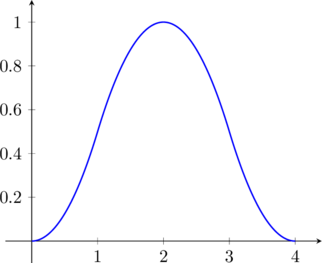
2) Considera la funzione:
(12) ![]()
con ![]() costante reale positiva; determina
costante reale positiva; determina ![]() in modo che
in modo che ![]() abbia lo stesso periodo di
abbia lo stesso periodo di ![]() .
.
Dimostra che la porzione quadrata di piano OABC in figura 1 viene suddivisa dai grafici di ![]() e
e ![]() in tre parti distinte e determina le probabilità che un punto preso a caso all’interno del quadrato OABC ricada in ciascuna delle 3 parti individuate.
in tre parti distinte e determina le probabilità che un punto preso a caso all’interno del quadrato OABC ricada in ciascuna delle 3 parti individuate.
Prerequisiti
- conoscere il significato di periodicità di una funzione trigonometrica
- conoscere la definizione di probabilità
- applicare il concetto di probabilità nel caso della geometria piana
- conoscere l’integrale come area di una regione finita di piano
Sviluppo
Perché la funzione (12) abbia periodo 4 è sufficiente studiare quando:
(13) ![]()
esso si annullerà quando:
(14) ![]()
avendo periodo 4 significa che sia per ![]() ma anche
ma anche ![]() si annulla per cui:
si annulla per cui:
(15) ![]()
entrambe mi portano ad affermare che
(16) ![]()
Rappresento graficamente la situazione per ![]() , ossia all’interno del quadrato
, ossia all’interno del quadrato ![]() .
.
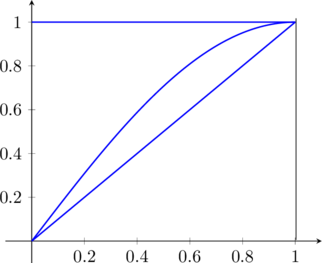
e si osserva che si hanno tre regioni.
La definizione di probabilità è:
(17) ![]()
In questo caso: l’evento favorevole è una delle tre aree, l’evento probabile è l’area totale che vale 1 essendo un quadrato di lato 1.
L’area della zona superiore si calcola sottraendo all’area del quadrato di lato unitario l’integrale della funzione ![]() :
:
(18) 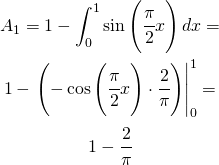
Essa corrisponde alla probabilità che il punto possa cadere in quest’area.
L’area della zona centrale si calcola attraverso l’integrale della funzione ![]() a cui sottraggo l’area del triangolo di base 1 ed uguale altezza.
a cui sottraggo l’area del triangolo di base 1 ed uguale altezza.
(19) 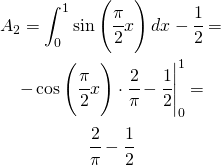
La terza area corrisponde all’area del triangolo di base 1 ed altezza unitaria:
(20) ![]()
3) Considerando ora le funzioni:
(21) ![]()
e
(22) ![]()
discuti, anche con argomentazioni qualitative, le variazioni (in aumento o in diminuzione) dei tre valori di probabilità determinati al punto precedente
Prerequisiti
- conoscenza del grafico del quadrato di una funzione e sua approssimazione grafica
- sapere sviluppare in maniera molto sicura gli integrali
Sviluppo
Tra ![]() la
la ![]() da retta diventa una parabola.
da retta diventa una parabola.
mentre la funzione trigonometrica ![]() ha un flesso per
ha un flesso per ![]() .
.
Si può quindi qualitativamente dire che
![]() diminuisce
diminuisce
![]() aumenta
aumenta
Per meglio evidenziare la situazione faccio il grafico delle tre curve che può essere ricavato solo se precedentemente ci si è esercitati con i grafici delle funzioni trigonometriche.
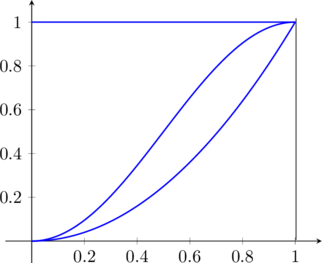
Per l’area compresa si deve calcolare il seguente integrale:
(23) 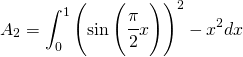
Vi sono due strade e la migliore è analizzare il grafico:
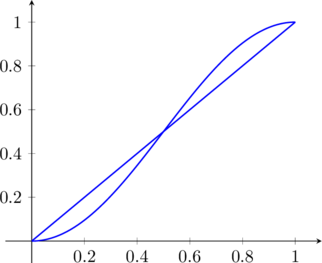
e si nota che l’area del grafico della funzione trigonometrica è proprio l’area del triangolo di base unitaria ed altezza uguale in quanto i contributi della “gobba” si bilanciano.
Quindi è sufficiente calcolare il seguente integrale notevolmente più semplice:
Per l’area compresa si deve calcolare il seguente integrale:
(24) 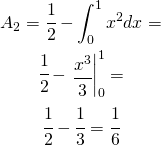
valore di poco inferiore a quello precedente.
4) Determina il volume del solido generato dalla rotazione attorno all’asse y della porzione di piano compresa tra il grafico della funzione ![]() per
per ![]() e l’asse x.
e l’asse x.
Prerequisiti
- conoscere la formula per il calcolo del volume di figure piane che ruotano attorno all’asse y.
Sviluppo
Si utilizza la seguente formula:
(25) ![]()
La applico ad ![]()
(26) 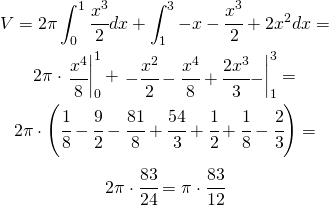
[:]
