[:it]Maturità 2017: secondo quesito[:]

Pubblicato il 25 Giugno 2017 da admin

[:it]

Andrea Wan

Una torta di forma cilindrica è collocata sotto una cupola di plastica di forma semisferica. Dimostrare che la torta occupa meno dei 3/5 del volume della semisfera.

Prerequisiti

  • conoscere il volume del cilindro e della sfera
  • trigonometria e disequazioni trigonometriche
  • studio di funzione

Sviluppo

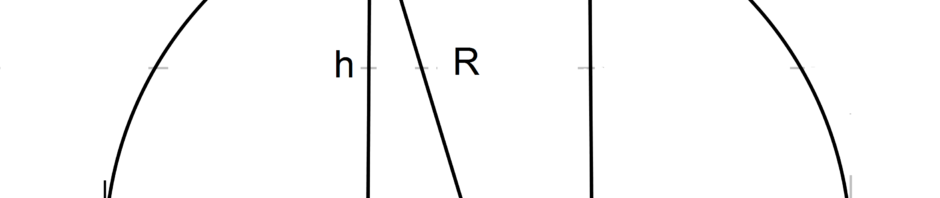
(1)   \begin{equation*} V_{torta}<\cfrac{3}{5}\cfrac{V_{sfera}}{2} \end{equation*}

Schematizzo il problema in questa maniera:

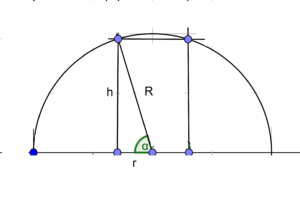
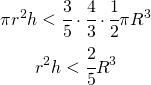
(2)   \begin{gather*} \pi r^{2} h<\cfrac{3}{5}\cdot \cfrac{4}{3}\cdot \cfrac{1}{2}\pi R^{3} \\ r^{2} h<\cfrac{2}{5}R^{3} \end{gather*}

(3)   \begin{gather*} h=R\sin \alpha \\ r=R\cos \alpha \\ \end{gather*}

sostituendo questo nella (2) devo dimostrare che:

(4)   \begin{gather*} R^{2}\cos^{2} \alpha \cdot R\sin \alpha < \cfrac{2}{5}R^{3} \\ \cos^{2} \alpha \cdot \sin \alpha < \cfrac{2}{5}\\ \left ( 1-\sin ^{2}\alpha \right )\cdot \sin \alpha < \cfrac{2}{5}\\ \sin \alpha -\sin ^{3}\alpha -\cfrac{2}{5}< 0 \end{gather*}

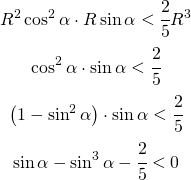
pongo \sin \alpha =t
con 0\leqslant \alpha \leqslant \cfrac{\pi}{2} e quindi 0\leqslant t \leqslant 1

devo risolvere:

(5)   \begin{gather*} 5t-5t^3-2< 0 \\ 5t^3-5t+2> 0 \\ \end{gather*}

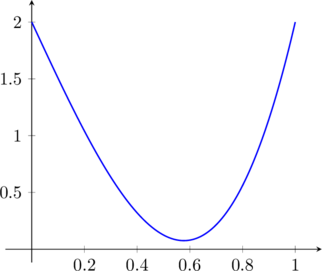
Effettuando uno studio di funzione di:

(6)   \begin{equation*} y=5t^3-5t+2 \end{equation*}

vedo che ha questo andamento per cui ho dimostrato l’affermazione del problema in quanto la funzione è sempre positiva nell’intervallo considerato

Rendered by QuickLaTeX.com

[:]

Questa voce è stata pubblicata in Senza categoria. Contrassegna il permalink.

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *