[:it]
Samy Charnine
E’ il caso in cui spesso si può trovare anche nell’ambito delle telecomunicazioni; se nella trasmissione di un fax , qual è la probabilità che essendo stato trasmesso un carattere bianco si possa avere un altro carattere bianco o un carattere nero?
In questo caso si è quindi nella situazione di probabilità subordinata o condizionata.
La probabilità che capiti l’evento A in seguito al fatto che si è verificato l’evento B è detta probabilità subordinata o probabilità condizionata e si indica con 
e si legge probabilità di A dato che si è verificato B.
Si può dimostrare facilmente che si calcola nella seguente maniera:
dove con 
si intende intersezione dei due eventi
in maniera analoga
.
Esempio:
E’ stata lanciata una moneta 3 volte ( o lanciate 3 monete in una volta sola). Qual è la probabilità che siano uscite tutte con la stessa faccia, sapendo che sono uscite meno di 2 teste?
La prima cosa che faccio è analizzare tutti i casi possibili del lancio di una moneta con i relativi risultati (esso si chiama spazio campionario o spazio degli eventi).
L’evento monete tutte con la stessa faccia A={
}
L’evento monete su tre lanci almeno due teste B={
}
[:]
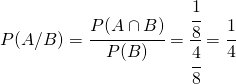