[:it]

Ivan Slavinsky
Siano dati dieci valori relativi ad una dimensione di un tavolo, ed altri dieci relativi all’altra dimensione (come da tabella 1). Si calcoli la superficie del tavolo considerando il relativo errore sulla misura, prendendo la corretta relazione che esprime le incertezza nella misura nel caso specifico.
Tabella 1 dei valori:
| Dimensione1 | Dimensione2 |
| 0.75 | 0.15 |
| 0.57 | 0.23 |
| 0.69 | 0.73 |
| 0.48 | 0.45 |
| 0.82 | 0.83 |
| 0.55 | 0.58 |
| 0.65 | 0.62 |
| 0.62 | 0.67 |
| 0.59 | 0.69 |
| 0.42 | 0.44 |
Per ogni dimensione si dovrà calcolare:
- il valore medio che è dato dalla somma dei valori diviso il numero dei valori
![]()
- l’errore massimo che è dato come la differenza tra il valore più grande ed il valore più piccolo
![]()
in generale quindi una grandezza si esprime come:
![]()
Tabella 2 che esprime i valori delle grandezze derivate e corrispondenti incertezze
| Grandezza | Valore più plausibile | Errore |
| a+b | Err(a)+Err(b) | |
| a-b | Err(a)+Err(b) | |
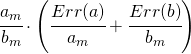 |
Specifiche di programmazione e relativo punteggio:
| Specifiche | Punteggio |
| Nome programma: CognomeNomeVergg_mm_aa
ad esempio RossiMarioVer27_11_17 |
0.2 |
| Commenti all’interno del programma che spieghi le singole fasi | 0.3 |
| Richiedere all’utente i dieci valori della tabella con la corretta istruzione di programmazione | 0.2 |
| Utilizzare un ciclo for o while per l’inserimento dei dati della prima dimensione (se non si riesce inserirli senza un ciclo) | 3 |
| Corretta gestione del tipo dei dati | 0.3 |
| Utilizzare un ciclo for o while per l’inserimento dei dati della seconda dimensione (se nel primo caso si è utilizzato un ciclo for nel secondo si usi un ciclo while o viceversa) | 3 |
| Utilizzare un ciclo for o while per determinare il valore minimo o massimo tra i valori inseriti | 2 |
| Calcolare il corretto algoritmo per il calcolo della superficie del tavolo | 1 |
[:]
