Una data funzione è esprimibile nella forma ![]() dove
dove ![]() e
e ![]() è un polinomio. Il grafico di
è un polinomio. Il grafico di ![]() interseca l’asse
interseca l’asse ![]() nei punti di ascisse
nei punti di ascisse ![]() e
e ![]() ed ha come asintoti le rette di equazioni
ed ha come asintoti le rette di equazioni ![]() ,
, ![]() e
e ![]() . Determinare i punti di massimo e di minimo relativi della funzione
. Determinare i punti di massimo e di minimo relativi della funzione ![]() .
.
Prerequisiti
- conoscere il significato degli asintoti in relazione alla forma di una funzione
- conoscere cosa rappresentano i punti che annullano il numeratore
- conoscere il concetto di derivata per il calcolo dei punti di massimo e di minimo
Sviluppo
Essendoci due asintoti verticali il denominatore si annullerà in 3 e -3.
Si può scrivere nella forma: ![]() .
.
Il numeratore si annulla in ![]() e
e ![]() per cui può essere scritto come:
per cui può essere scritto come: 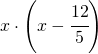 ; si deve inserire l’ulteriore condizione che è presente un asintoto orizzontale in
; si deve inserire l’ulteriore condizione che è presente un asintoto orizzontale in ![]() .
.
Per avere tale asintoto è sufficiente moltiplicare il numeratore per 5 che risulterà quindi:
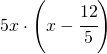 .
.
Ricapitolando le affermazioni precedenti la funzione, affinché soddisfi i vincoli dati si può scrivere nella forma:
![]() .
.
Adesso di calcoli la sua derivata prima per la determinazione dei massimi e dei minimi:
![]()
I valori in cui si annulla il numeratore sono ![]() e
e ![]() .
.
Studiando il segno della derivata prima si ha che è positiva per ![]() e
e ![]() per cui il massimo della funzione si ha in
per cui il massimo della funzione si ha in ![]() ed il massimo in
ed il massimo in ![]() .
.
Sostituendo tali valori nella funzione di partenza si avrà il punto di massimo:
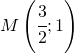
ed il punto di minimo:
![]()
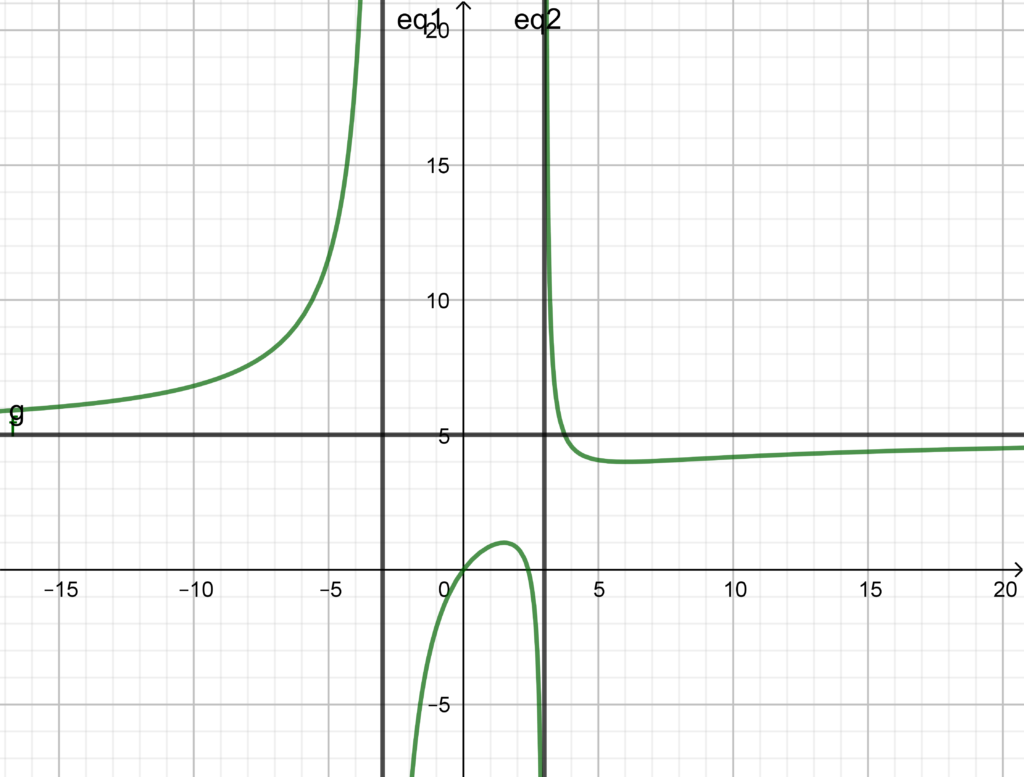
Il grafico della funzione, anche se non richiesto risulta: