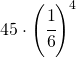Si lanciano 4 dati con facce numerate da 1 a 6:
- Qual è la probabilità che la somma dei 4 numeri usciti non superi il 5?
- Qual è la probabilità che il prodotto dei 4 numeri usciti sia multiplo di 3?
- Qual è la probabilità che il massimo numero uscito sia 4?
Prerequisito
- conoscere bene le permutazioni con ripetizione
- lo schema ad albero per calcolare le probabilità del prodotto e somma di eventi
Sviluppo
Primo punto:
Per avere che la somma non superi il 5 è necessario che si abbia la seguente quaterna:
1 1 1 2
essa può essere vista come una permutazione con ripetizione del gruppo 1 tre volte e quindi le possibili permutazioni sono:
![]()
ed anche la quaterna
1 1 1 1
La probabilità che esca 1 è \cfrac{1}{6} come pure che esca il 2 e quindi si deve effettuare il prodotto affinché esca la quaterna 1 1 1 2 ossia
![]()
siccome può capitare quattro volte, la probabilità cercata sarà:
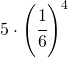
Secondo punto:
Il ragionamento è molto simile al precedente
per avere che il prodotto sia un multiplo del 3 si dovranno avere queste quaterne (a fianco inserisco quante possibili permutazioni possono essere inserite e elativa probabilità:
| Quaterna | permutazione | probabilità |
| 6 3 3 3 | 4 | 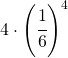 |
| 6 6 6 6 | 1 | |
| 1 1 1 3 | 4 | 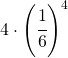 |
| 6 1 1 1 | 4 | 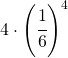 |
| 6 6 6 3 | 4 | 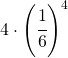 |
| 6 6 3 3 | 6 | 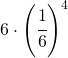 |
Si sommano adesso tutte le probabilità e si ha:
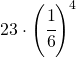
terzo punto:
Seguo il ragionamento e lo schema precedente:
| quaterna | permutazione | probabilità |
| 4 1 1 1 | 4 | 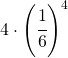 |
| 4 2 2 2 | 4 | 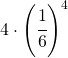 |
| 4 3 3 3 | 4 | 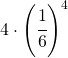 |
| 4 4 4 4 | 1 | 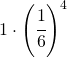 |
| 4 1 2 2 | 6 | 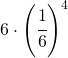 |
| 4 1 1 2 | 6 | 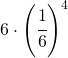 |
| 4 1 3 3 | 6 | 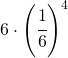 |
| 4 1 1 3 | 6 | 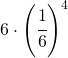 |
| 4 2 2 3 | 6 | 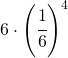 |
| 4 2 3 3 | 6 | 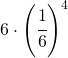 |
Si sommano adesso tutte le probabilità e si ha: