Un condensatore piano è formato da due armature circolari di raggio R, poste a distanza d, dove R e d sono espresse in metri (m). Viene applicata alle armature una differenza di potenziale variabile nel tempo e inizialmente nulla.
All’interno del condensatore si rileva la presenza di un campo magnetico B.
Trascurando gli effetti di bordo, a distanza r dall’asse di simmetria del condensatore, l’intensità di B, espressa in tesla(T), varia secondo la legge:
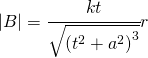con 
dove 
e 
sono costanti positive e 
è il tempo trascorso dall’istante iniziale, espresso in secondi (s).
- Dopo aver determinato le unità di misura di a e k
- spiegare perché nel condensatore è presente un campo magnetico anche in assenza di magneti e correnti di conduzione
- Qual è la relazione tra le direzioni di B e del campo elettrico E nei punti interni al condensatore?
Prerequisiti
- conoscenza delle unità di misura che caratterizzano il campo induzione magnetica
- conoscenza della legge di Ampere Maxwell o quarta equazione di Maxwell.
Sviluppo
Primo punto
Si parte dalla relazione espressa solo in funzione delle unità di misura:
![[T]=k\cfrac{[s][m]}{\sqrt{([s]^2)^3}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-78c527c07cae815fd46483f078dcf60c_l3.png "Rendered by QuickLaTeX.com")
dove è espressa inevitabilmente in secondi.
Per cui ![k=\cfrac{[T][s]^2}{[m]}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9341953ae05e6fd1fc037540c21ed0c7_l3.png "Rendered by QuickLaTeX.com")
Secondo punto
Si applica la legge di Ampere-Maxwell considerando nullo le correnti che non sono presenti in questo caso:
essendovi la circuitazione vi è il campo magnetico.
Terzo punto
Le linee di campo elettrico sono perpendicolari alle armature mentre quelle di campo magnetico sono concentriche rispetto al centro del condensatore e sono perpendicolari a quelle elettriche.