Nell’interesse semplice il capitale aumenta seguendo la seguente relazione:
![]()
in cui i dati numerici sono C che è il Capitale ad esempio 1000€, ed i che è il tasso di interesse sempre espresso in percentuale ad esempio 10%
Le variabili che cambiano nel tempo sono quindi il capitale finale ed il tempo.
Lo scopo è quello di usare un foglio excel per rappresentare l’aumento del capitale al trascorrere del tempo e farne il relativo grafico.
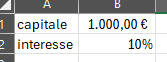
- nella cella A1 scrivere Capitale
- nella cella B1 inserire 1000 formato valuta
- nella cella A2 scrivere Interesse
- formattare la cella B2 con il formato percentuale
- inserire il valore 10
Ci si troverà in questa situazione:
- nella cella D4 scrivere tempo
- nella cella E4 scrivere montante
- nella cella D5 scrivere 1
- nella cella D2 scrivere =D5+1
- adesso puntare la cella D2 che presenterà un contorno verde e mettere il puntatore del mouse sull’angolo in basso a destra finchè il puntatore non presenterà la forma di una croce. A questo punto tenendo premuto il pulsante sinistro del mouse trascinare i valori fono al valore 17.
- inserire nella cella E5 la seguente formula
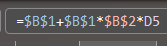
Andare a completare anche questa colonna. Ci si troverà in questa situazione:
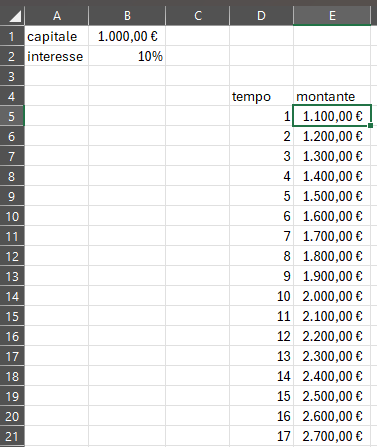
Si vogliono rappresentare queste due colonne su un grafico.
Sei selezionano entrambe tenendo premuto il pulsante sinistro del mouse e poi lo si rilascia.
Si va su inserisci grafici a dispersione e si seleziona il primo, lo si rilascia e ci troverà in questa situazione finale.
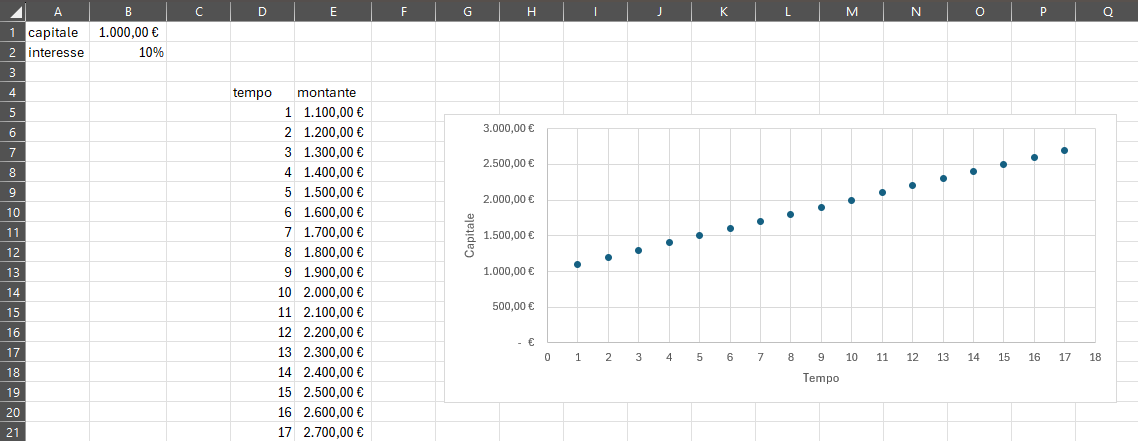
Conclusione
L’interesse semplice permette una crescita lineare del capitale ma è solo una soluzione ideale e non reale. Lo si analizzerà quando si affronterà l’interesse composto.
