E’ assegnata la funzione:
![]()
Provare che esiste un solo ![]() tale che
tale che ![]() . Determinare inoltre:
. Determinare inoltre:
![]() .
.
Prerequisiti
- definizione di funzione dispari
- analisi della crescenza e decrescenza di una funzione dalla sua derivata
- applicazione di De L’Hospital o la conoscenza degli infinitesimi per lo sviluppo del limiti
Sviluppo
La funzione è una funzione dispari ossia:
![]()
infatti:
![]()
e
![]()
quindi è simmetrica rispetto all’origine.
Inoltre facendo la derivata prima di ![]() si ha:
si ha:
![]()
che è la somma di soli termini positivi per cui è sempre positiva e quindi la funzione è sempre crescente.
Simmetrica e sempre crescente esisterà solo un punto che la annulla che sarà poi proprio l’origine.
Anche se il grafico non è richiesto il grafico infatti risulta:
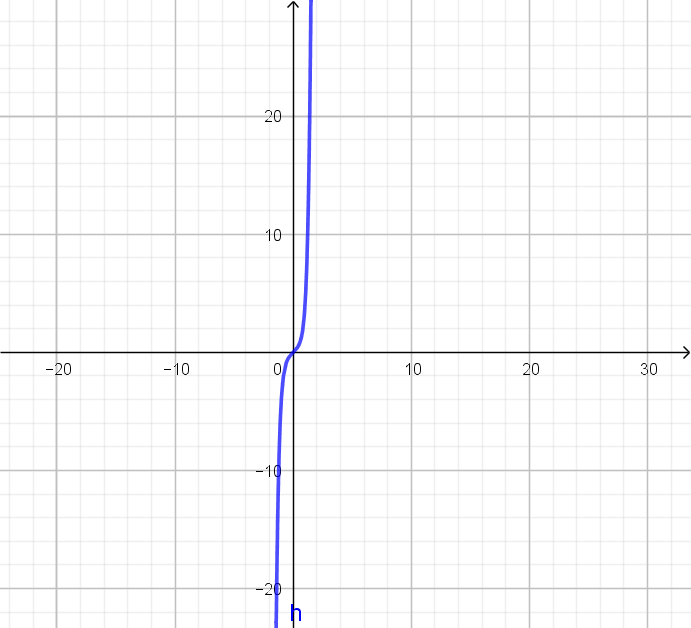
Adesso si passa a calcolare il limite.
Siccome si è nella forma infinito su infinito applico De l’Hospital:
![]() .
.
Iterando De L’Hospital 2018 volte mi troverò un numero diviso ![]() e quindi il limite assumerà il valore
e quindi il limite assumerà il valore ![]() .
.
![]() .
.
