Dati i punti 
e 
, provare che il luogo geometrico dei punti P dello spazio, tali che, 
, è costituito da una superficie sferica S e scrivere la sua equazione cartesiana. Verificare che il punto 
appartenga ad S e determinare l’equazione del piano tangente in T ad S.
Prerequisiti
- conoscenza della distanza tra due punti nello spazio
- definizione di raggio e centro di una sfera
- conoscenza della retta passante per due punti nello spazio
- conoscenza della relazione tra vettore direzione della retta e di quello del piano
- conoscenza condizione di appartenenza di un punto nello spazio.
Sviluppo
Per prima cosa impongo la condizione .
elevando tutto al quadrato e sviluppando i quadrati del binomio si ha:
sommando i monomi simili ed ordinandoli nella forma della sfera si ha:
per dimostrare che rappresenti una sfera i coefficienti dei termini al quadrato devono essere uguali: ciò è soddisfatto; inoltre il valore del raggio deve dare un valore maggiore di zero. Le coordinate del centro sono:
e quelle del raggio sono:
quindi è proprio l’equazione di una sfera:
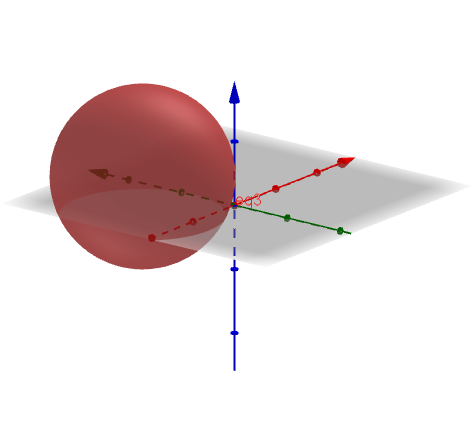
Per verificare che il punto appartenga alla sfera è sufficiente sostituire le sue coordinate all’equazione della sfera e verificare che si abbia un’identità.
ed infatti è un’identità:
Adesso determino la retta passante per il centro e per il punto 
.
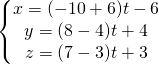
quindi il vettore direzione ha componenti v(-4,4,4) che sono le stesse componenti del vettore direzione del piano perpendicolare a tale retta.
L’equazione del piano sarà quindi:
il piano passa per il punto , per cui è sufficiente sostituire le sue coordinate per determinare d:
ed il piano avrà equazione:
oppure semplificando:
