Un protone penetra in una regione di spazio in cui è presente un campo magnetico uniforme di modulo 
.
Esso inizia a muoversi descrivendo una traiettoria ad elica cilindrica, con passo costante 
, ottenuta dalla composizione di un moto circolare uniforme di raggio r=10.5 cm e di un moto rettilineo uniforme. Determinare il modulo del vettore velocità e l’angolo che esso forma con 
.
Prerequisiti
- conoscenza della forza di Lorentz
- moto circolare
- scomposizione dei vettori velocità
Sviluppo
Forza di Lorentz
Essendo un moto elicoidale si deve tener presente questo schema:
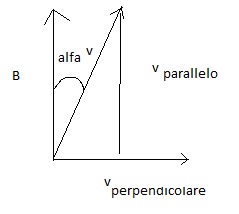
ossia la formula precedente diventa in modulo
per cui quella precedente diventa:
ma il periodo T:
da cui si trova:
.