Si assuma,d’ora in avanti, di avere ![]() e
e ![]() .
.
- Studiare le due funzioni così ottenute
- verificando che il grafico di
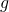 ammette un centro di simmetria
ammette un centro di simmetria - i grafici di
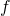 e
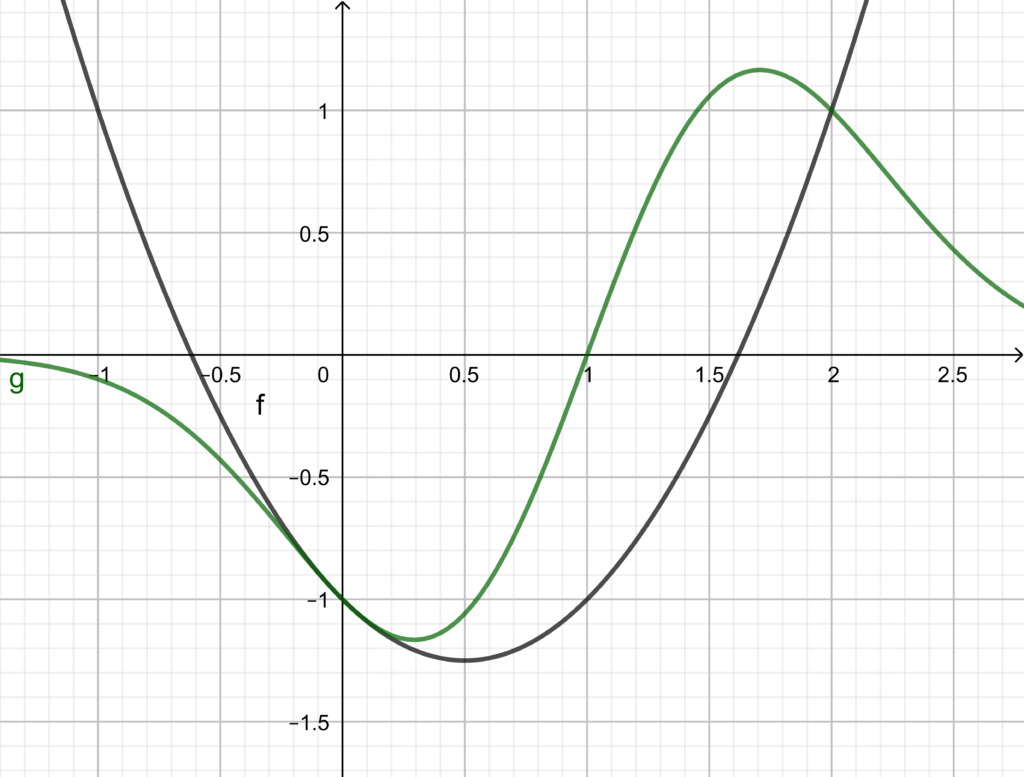
e 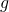 sono tangenti nel punto B(0,−1)
sono tangenti nel punto B(0,−1) - determinare inoltre l’area della regione piana S delimitata dai grafici delle funzioni
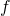 e
e 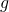 .
.
Prerequisiti
- saper fare lo studio di funzione
- ricordare la condizione per il centro di simmetria di una curva
- risolvere un sistema uguagliando al parte esponenziale con la parte non esponenziale
- saper calcolare un integrale definito: area racchiusa tra due curve
Sviluppo
Primo punto
Parto con la ![]() che è una semplice parabola.
che è una semplice parabola.
Le intersezione con l’asse ![]() ossia ponendo
ossia ponendo ![]() risulta -1.
risulta -1.
L’intersezioni con l’asse ![]() ossia ponendo
ossia ponendo ![]() e risolvendo l’equazione di secondo grado
e risolvendo l’equazione di secondo grado ![]() sono:
sono:
![]() e
e
![]()
Con la derivata prima determino il vertice della parabola:
![]()
Il vertice della parabola risulta:
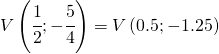
è un punto di minimo (basta studiare il segno della derivata prima.
Adesso studio la ![]() .
.
L’intersezione con l’asse ![]() ossia ponendo
ossia ponendo ![]() risulta -1.
risulta -1.
L’intersezione con l’asse ![]() ossia ponendo
ossia ponendo ![]() risulta 1.
risulta 1.
Studio la derivata prima e di ha dopo alcuni semplici passaggi:
![]()
![]()
![]()
Studiando il segno si vede che il primo è il punto di massimo mentre il secondo è il punto di minimo con le seguenti coordinate.
minimo ![]() e massimo
e massimo ![]()
La rappresentazione grafica fornisce le seguenti curve:
Secondo punto
Perchè esista un centro di simmetria deve valere la seguente relazione:
![]()
sostituendoli nella ![]() risulta:
risulta:
![]()
e bisogna uguagliarle:
![]()
da questa si vede che ![]() e guardando solo i termini che non sono nell’esponente si ha la condizione
e guardando solo i termini che non sono nell’esponente si ha la condizione ![]() ossia
ossia ![]() .
.
il punto ![]() è quello di simmetria. Come si poteva anche vedere dal grafico
è quello di simmetria. Come si poteva anche vedere dal grafico
Terzo punto
Si deve risolvere il sistema:
![]()
![]()
L’esponenziale si deve annullare per cui:
![]() che ha come soluzioni 0 e 2
che ha come soluzioni 0 e 2
Anche il polinomi che moltiplica l’esponenziale si deve annullare
![]() che ha come soluzione o e 2.
che ha come soluzione o e 2.
Quindi si annulla in ![]() e in
e in ![]() .
.
Per verificare la condizione di tangenza si calcola il valore della derivata prima in 0 e deve avere lo stesso valore:
![]()
![]()
![]()
![]()
ed effettivamente sono tangenti.
Quarto punto
Si deve calcolare l’area della seguente regione di piano:
![]()
Si deve notare che il primo integrale (x-1) è la derivata a meno di -2 dell’esponente per cui la primitiva risulta:
![]()
![]() .
.
