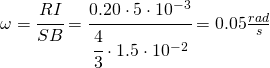Si supponga, in assenza dei tre fili, che il contorno della regione S rappresenti il profilo di una spira conduttrice di resistenza R = 0,20 Ω. La spira è posta all’interno di un campo magnetico uniforme di intensità 
perpendicolare alla regione S. Facendo ruotare la spira intorno all’asse x con velocità angolare ω costante, in essa si genera una corrente indotta la cui intensità massima è pari a 5,0mA. Determinare il valore di ω.
Prerequisiti
- conoscenza della legge di Faraday Neumann applicata ad una superficie in rotazione che è equivalente ad un campo magnetico sinusoidale.
Sviluppo
La legge di Faraday Neumann dice che:
è costante
ed è l’unico termine che varia con il tempo per cui la sua derivata risulta:
che sostituita nell’equazione di partenza si ha:
Siccome si ha il valore massimo:
