- Con le opportune motivazioni, dedurre il grafico di
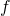da quello di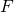 
- specificando cosa rappresentano le ascisse dei punti di flesso di F per la funzione f.
- Calcolare l’area della regione compresa tra il grafico di 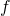, l’asse delle ascisse e le rette parallele all’asse delle ordinate passanti per gli estremi della funzione.
- Fissato b > 0, calcolare il valore di:
Prerequisiti
- analisi di un grafico partendo dalla sua primitiva
- analisi dei punti di flesso in rapporto alla sua derivata
- saper integrare
Sviluppo
Primo punto
Osservando la concavità si osserva dove la derivata prima è positiva ed è negativa.
Lo zero è il punto che annulla la derivata prima ed è il punto di massimo
Secondo punto
Le ascisse dei punti di flesso rappresentano i punti di massimo e di minimo del grafico della derivata prima.
Si ha il seguente grafico:
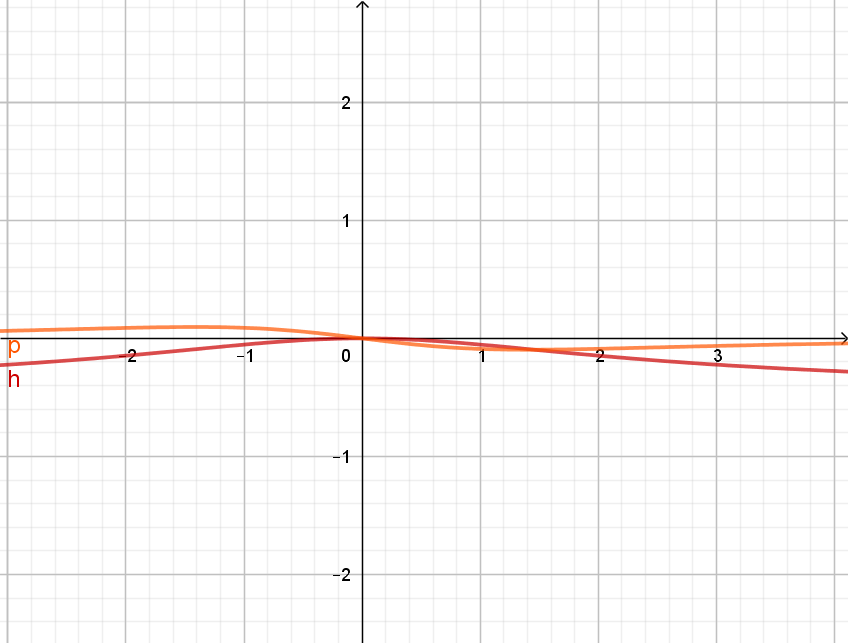
Terzo punto
La è simmetrica per cui è sufficiente calcolare:
Quarto punto
essendo la funzione simmetrica