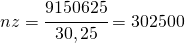Renè Magritte – 1935 – “La condizione umana”
(1.a) 
(1.b) 
(1.c) 
(1.d) 
(1.e) 
(1.f) 
(1.g) 
(2.a) 
(2.b) 
(2.c) 
(2.d) 
(2.e) 
(2.f) 
(3.a)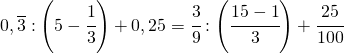 
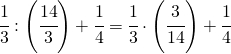
(3.b)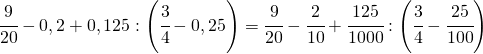 
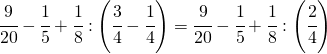
(3.c)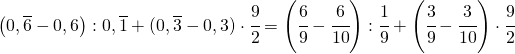 
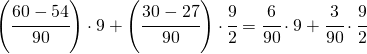
(4) Leggendo il testo si nota che tutti i dati si riferiscono a promossi a prescindere che questi lo siano stati a giugno (“per merito”) o a settembre(“debito formativo”). Sommo le rispettive percentuai e trovo che 
ossia la totalità è stata promossa. I respinti quindi non ve ne saranno.
(5) 
(6) Il perimetro è datto da 
(7) Area del triangolo isocele 
sostituendo i valori dati ho: 
Per determinare il perimetro devo trovare il valore dei lati obliqui ossia applicare il teorema di pitagora conoscendo la lunghezza dei due cateti che sono entrambi 5. Infatti metà della base lunga 10 fa proprio 5.
Il perimetro sarà quindi:
(8) Si ha un trapezio scaleno ossia con tutti e quattro i lati diversi. Il perimetro è la somma dei quattro lati:
Alla base delle attuali conoscenza non si riesce a calcolare l’altezza per cui per calcolare l’area manca il dato sull’altezza.
(9) Partendo dalla domanda.
- Devo coprire un’area con le singole zolle di cui ho le dimensioni.
- L’area coperta da ogni singola zolla è:
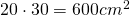. Se conosco l’area che dovrò coprire posso dividerla per l’area coperta da ogni singola piastrella .
- Dell’area conosco il perimetro e la forma.
- Dal perimetro e sapendo che è un quadrato conosco il lato
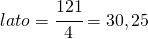
- Adesso posso calcolare l’area ossia
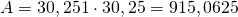
- Adesso divido l’area dell’appezzamento per l’area della singola zolla ricordandomi che la zolla è in
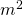
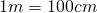per cui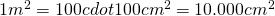 
- L’area da coprire con le zolle è
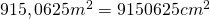
- Il risultato è
