(1) ![Rendered by QuickLaTeX.com \cfrac{\left(\cfrac{3}{4}-0,0\overline{3}\right)\cdot\cfrac{3}{43}+\left(2,\overline{4}-1,2\right)\cdot\cfrac{9}{7}-\cfrac{8}{5}}{\left[\cfrac{2,3-2,\overline{15}}{0,2+1,\overline{3}}\cdot\left(5+\cfrac{8}{49}\right)+\cfrac{3}{4}\right]:\left(1+\cfrac{1}{4}\right)}+\cfrac{4}{0,\overline{2}+1,2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-02d65e94d0917de7b9476a0094a75a18_l3.png)
quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{3}{4}-\cfrac{3}{90}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{24-2}{9}-\cfrac[l]{12}{10}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{215-2}{99}}{\cfrac{2}{10}+\cfrac{13-1}{9}}\cdot\left(5+\cfrac{8}{49}\right)+\cfrac{3}{4}\right]:\left(\cfrac{5}{4}\right)}+\cfrac{4}{\cfrac{2}{9}+\cfrac{12}{10}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-28424d303d5ce665cd63a30d935d0762_l3.png)
quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{3}{4}-\cfrac{1}{30}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{22}{9}-\cfrac[l]{6}{5}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{213}{99}}{\cfrac{1}{5}+\cfrac{12}{9}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{4}{\cfrac{20+108}{90}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-06555bd3c875b67329729bd153b46c89_l3.png)
passaggio successivo
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{45-2}{60}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{110-54}{45}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{71}{33}}{\cfrac{1}{5}+\cfrac{12}{9}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{4}{\cfrac{128}{90}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e3ec27b70796301863401cdf0ea8bf38_l3.png)
e quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{43}{60}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{56}{45}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{759-710}{330}}{\cfrac{9+60}{45}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+4\cdot\cfrac{90}{128}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9f9bb9ead11586bffd4188482c94e631_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}+\cfrac{8}{5}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{49}{330}}{\cfrac{69}{45}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-8e9af0d21b6955edb5cbb40dca7c8a6b_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{49}{330}\cdot\cfrac{45}{69}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-79d070175d19f76c39957311f4a0d823_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{1}{2}+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-4df53411cdfe99cd68512672fe340b24_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{5}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ab6f29207a5418baa8c16b081937aeea_l3.png)
e
![]()
ed infine
![]()
(2) ![Rendered by QuickLaTeX.com \cfrac{\left[\left(2+\cfrac{1}{2}\right)^{2}\cdot\left(3-\cfrac{4}{3}\right)^{2}\cdot\left(-1-\cfrac{1}{5}\right)^{2}\right]^{-1}:\left(-1+\cfrac{4}{5}\right)^{2}}{\cfrac{1}{2}\cdot\left(-\cfrac{1}{3}\right)^{-2}+\left(\cfrac{1}{4}\right)^{2}\cdot\left(1-\cfrac{3}{8}\right)^{-2}:\left(1-\cfrac{3}{5}\right)^{2}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3622f616b5ce34a9e5c15ffa6f238d29_l3.png)
Risultato ![]()
![Rendered by QuickLaTeX.com \cfrac{\left[\left(\cfrac{5}{2}\right)^{2}\cdot\left(\cfrac{5}{3}\right)^{2}\cdot\left(-\cfrac{6}{5}\right)^{2}\right]^{-1}:\left(-\cfrac{1}{5}\right)^{2}}{\cfrac{1}{2}\cdot9+\cfrac{1}{4^{2}}\cdot\left(\cfrac{5}{8}\right)^{-2}:\left(\cfrac{2}{5}\right)^{2}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a6b6425e1de27a0a44f4b98eef018394_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac{\left[\cfrac{5^{2}}{2^{2}}\cdot\cfrac{5^{2}}{3^{2}}\cdot\cfrac{6^{2}}{5^{2}}\right]^{-1}\cdot5^{2}}{\cfrac{9}{2}+\cfrac{1}{4^{2}}\cdot\cfrac{8^{2}}{5^{2}}\cdot\cfrac{5^{2}}{2^{2}}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d384a8e0549ec3dc52748f4931cbb4cf_l3.png)
ed infine
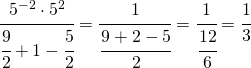
Come conclusione
[paypal-donation]
(1) ![Rendered by QuickLaTeX.com \cfrac{\left(\cfrac{3}{4}-0,0\overline{3}\right)\cdot\cfrac{3}{43}+\left(2,\overline{4}-1,2\right)\cdot\cfrac{9}{7}-\cfrac{8}{5}}{\left[\cfrac{2,3-2,\overline{15}}{0,2+1,\overline{3}}\cdot\left(5+\cfrac{8}{49}\right)+\cfrac{3}{4}\right]:\left(1+\cfrac{1}{4}\right)}+\cfrac{4}{0,\overline{2}+1,2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-02d65e94d0917de7b9476a0094a75a18_l3.png)
quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{3}{4}-\cfrac{3}{90}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{24-2}{9}-\cfrac[l]{12}{10}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{215-2}{99}}{\cfrac{2}{10}+\cfrac{13-1}{9}}\cdot\left(5+\cfrac{8}{49}\right)+\cfrac{3}{4}\right]:\left(\cfrac{5}{4}\right)}+\cfrac{4}{\cfrac{2}{9}+\cfrac{12}{10}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-28424d303d5ce665cd63a30d935d0762_l3.png)
quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{3}{4}-\cfrac{1}{30}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{22}{9}-\cfrac[l]{6}{5}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{213}{99}}{\cfrac{1}{5}+\cfrac{12}{9}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{4}{\cfrac{20+108}{90}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-06555bd3c875b67329729bd153b46c89_l3.png)
passaggio successivo
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{45-2}{60}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{110-54}{45}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{71}{33}}{\cfrac{1}{5}+\cfrac{12}{9}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{4}{\cfrac{128}{90}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e3ec27b70796301863401cdf0ea8bf38_l3.png)
e quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{43}{60}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{56}{45}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{759-710}{330}}{\cfrac{9+60}{45}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+4\cdot\cfrac{90}{128}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9f9bb9ead11586bffd4188482c94e631_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}+\cfrac{8}{5}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{49}{330}}{\cfrac{69}{45}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-8e9af0d21b6955edb5cbb40dca7c8a6b_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{49}{330}\cdot\cfrac{45}{69}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-79d070175d19f76c39957311f4a0d823_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{1}{2}+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-4df53411cdfe99cd68512672fe340b24_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{5}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ab6f29207a5418baa8c16b081937aeea_l3.png)
e
![]()
ed infine
![]()
(2) ![Rendered by QuickLaTeX.com \cfrac{\left[\left(2+\cfrac{1}{2}\right)^{2}\cdot\left(3-\cfrac{4}{3}\right)^{2}\cdot\left(-1-\cfrac{1}{5}\right)^{2}\right]^{-1}:\left(-1+\cfrac{4}{5}\right)^{2}}{\cfrac{1}{2}\cdot\left(-\cfrac{1}{3}\right)^{-2}+\left(\cfrac{1}{4}\right)^{2}\cdot\left(1-\cfrac{3}{8}\right)^{-2}:\left(1-\cfrac{3}{5}\right)^{2}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3622f616b5ce34a9e5c15ffa6f238d29_l3.png)
Risultato ![]()
![Rendered by QuickLaTeX.com \cfrac{\left[\left(\cfrac{5}{2}\right)^{2}\cdot\left(\cfrac{5}{3}\right)^{2}\cdot\left(-\cfrac{6}{5}\right)^{2}\right]^{-1}:\left(-\cfrac{1}{5}\right)^{2}}{\cfrac{1}{2}\cdot9+\cfrac{1}{4^{2}}\cdot\left(\cfrac{5}{8}\right)^{-2}:\left(\cfrac{2}{5}\right)^{2}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a6b6425e1de27a0a44f4b98eef018394_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac{\left[\cfrac{5^{2}}{2^{2}}\cdot\cfrac{5^{2}}{3^{2}}\cdot\cfrac{6^{2}}{5^{2}}\right]^{-1}\cdot5^{2}}{\cfrac{9}{2}+\cfrac{1}{4^{2}}\cdot\cfrac{8^{2}}{5^{2}}\cdot\cfrac{5^{2}}{2^{2}}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d384a8e0549ec3dc52748f4931cbb4cf_l3.png)
ed infine
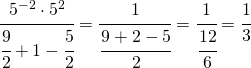
Come conclusione
[paypal-donation]