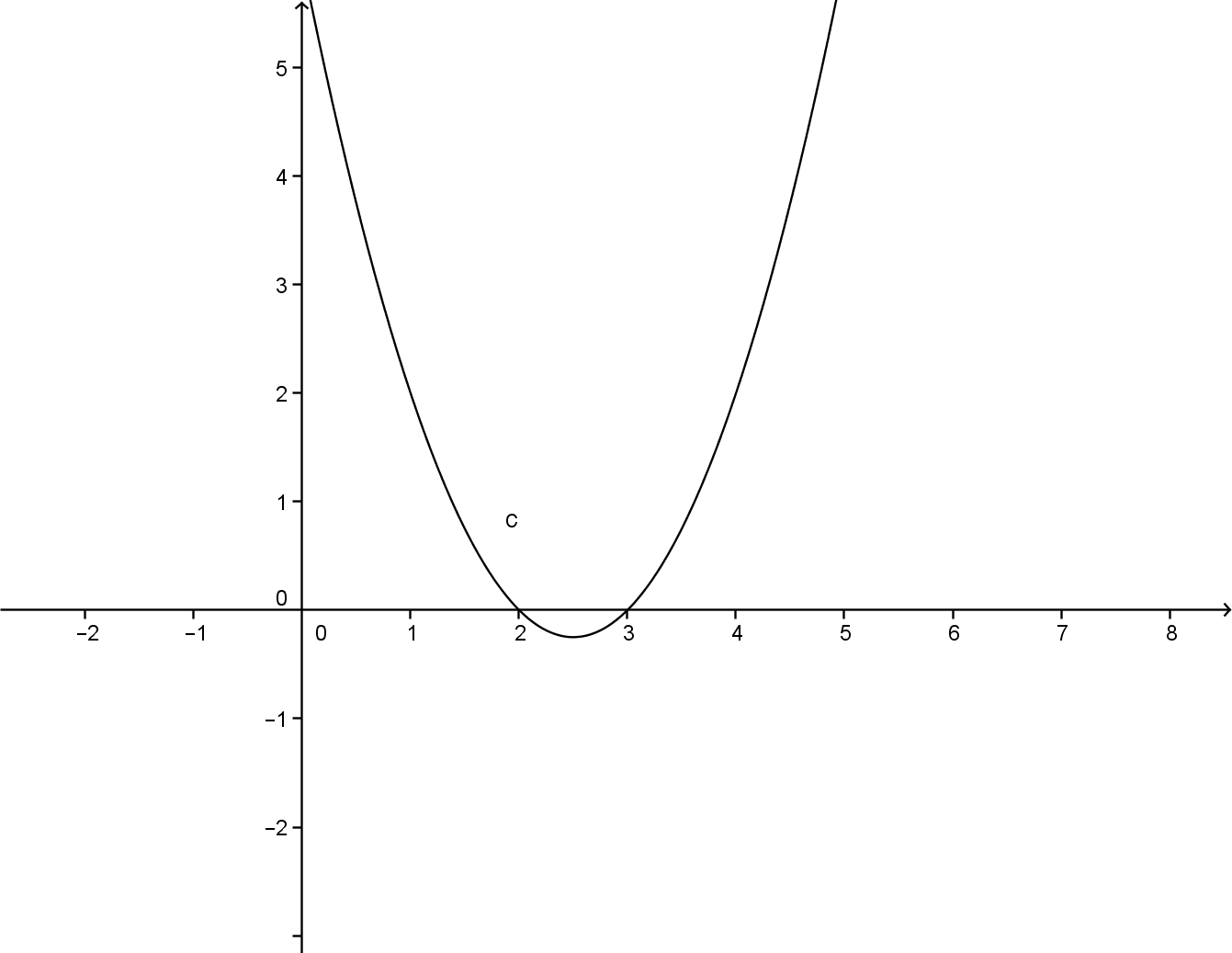
Una volta che si riesce a calcolare la derivata prima di una funzione si può cominciare ad intuire come potrà essere il suo grafico. In particolare siccome la derivata prima fornisce il valore dell’inclinazione della curva tangente si può capire che quando essa si annulla la relativa retta è orizzontale.
Una volta che si riesce a calcolare la derivata prima di una funzione si può cominciare ad intuire come potrà essere il suo grafico. In particolare siccome la derivata prima fornisce il valore dell’inclinazione della curva tangente si può capire che quando essa si annulla la relativa retta è orizzontale.
A questo punto posso, studiando il segno della derivata prima capire quando cresce e quando decresce la funzione.
Partendo dall’esempio più banale che possa esserci cerco di chiarire il concetto.
Sia ![]() .
.
Calcolo la derivata prima:
![]()
Il punto in cui si annulla si ottiene annullando la derivata prima:
![]()
ossia
![]()
Esso è un punto di massimo o minimo?
Risolvo la disequazione
![]()
Essa è positiva per
![]()
E’ facilmente dimostrabile che quando la derivata prima è negativa la funzione è decrescente e quando la derivata prima è positiva è crescente.
Per cui la mia funzione di partenza (parabola) è:
- decrescente per
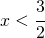
- crescente per
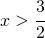
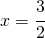 è il punto di minimo (in questo caso anche assoluto della funzione).
è il punto di minimo (in questo caso anche assoluto della funzione).
Per trovare il valore della relativa ordinata del punto di minimo si sostituisce alla funzione di partenza il valore trovato:
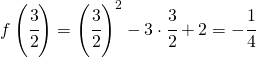
Ossia il punto di minimo ha coordinate:
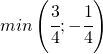
Il grafico della funzione è: