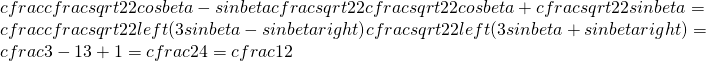3) Dato ![]() che appartengono al primo quadrante e che:
che appartengono al primo quadrante e che:
![]()
![]()
Dimostrare che:
![]()
Sviluppo
(1) ![]()
![]() ossia
ossia
(2) ![]()
Adesso utilizzo la (1)
![Rendered by QuickLaTeX.com tanalpha=cfrac{sinalpha}{cosalpha}=cfrac{sinleft(cfrac[l]{pi}{4}-betaright)}{cosleft(cfrac{pi}{4}-betaright)}=cfrac{sincfrac{pi}{4}cosbeta-sinbetacoscfrac{pi}{4}}{coscfrac{pi}{4}cosbeta+sincfrac{pi}{4}sinbeta}=cfrac{1}{2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a10f0ac6db51364ed3da397a95eb06ba_l3.png)
quindi utilizzando anche la (2) e sviluppando il seno di 45° ed il coseno di 45° ho:
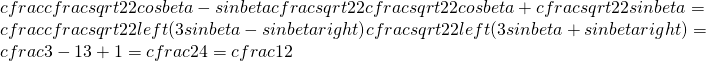

3) Dato ![]() che appartengono al primo quadrante e che:
che appartengono al primo quadrante e che:
![]()
![]()
Dimostrare che:
![]()
Sviluppo
(1) ![]()
![]() ossia
ossia
(2) ![]()
Adesso utilizzo la (1)
![Rendered by QuickLaTeX.com tanalpha=cfrac{sinalpha}{cosalpha}=cfrac{sinleft(cfrac[l]{pi}{4}-betaright)}{cosleft(cfrac{pi}{4}-betaright)}=cfrac{sincfrac{pi}{4}cosbeta-sinbetacoscfrac{pi}{4}}{coscfrac{pi}{4}cosbeta+sincfrac{pi}{4}sinbeta}=cfrac{1}{2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a10f0ac6db51364ed3da397a95eb06ba_l3.png)
quindi utilizzando anche la (2) e sviluppando il seno di 45° ed il coseno di 45° ho: