Un asintoto oltre che verticale può essere anche orizzontale, ossia parallelo all’asse delle ascisse.
Per la sua presenza deve valere la seguente relazione:
(1) ![]()
La (1) afferma che quando x assume valori molto grandi, infinitamente grandi, la funzione tende a un valore finito ossia ad un asintoto orizzontale.
Ecco alcuni esempi della presenza di asintoti verticali:
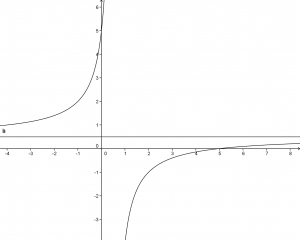
(2) ![]()
in questo caso la (2) ci fornisce un asintoto orizzontale con valore
![]()
Per meglio evidenziare tale fatto ecco il grafico della funzione:
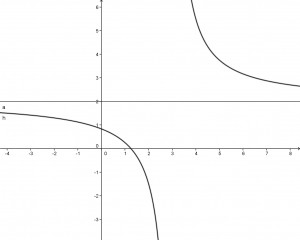
(3) ![]()
in questo caso l’asintoto è:
![]()
Ecco il grafico della funzione: