Equazioni di primo grado a coefficienti frazionari

Pubblicato il 21 Settembre 2012 da admin

[:it]

Pablo Picasso

Pablo Picasso

Per sviluppare queste equazioni è indispensabile conoscere bene le operazioni con le frazioni .

Esercizi di base

In questi esercizi ci si deve ricordare la regola empirica ossia se voglio che la x rimanga con coefficiente numerico positivo ed intero (ossia 1) è sufficiente “trasportare” la frazione di sinistra, a destra del simbolo di “=” ma essa CAMBIA DI SEGNO.

Ad esempio:

x - \cfrac{3}{4}=\cfrac{2}{4}

x=\cfrac{2}{4}+\cfrac{3}{4}

x=\cfrac{5}{4}

A.1. x + \cfrac{5}{6}=\cfrac{8}{6} \left [ \cfrac{1}{2} \right ]
A.2. x - \cfrac{1}{4}=\cfrac{3}{4} \left [ 1 ]
A.3. x - \cfrac{1}{5}=\cfrac{4}{5} \left [1]
A.4. x - \cfrac{3}{2}=\cfrac{5}{2} \left [4]
A.5. x - \cfrac{7}{3}=\cfrac{10}{3} \left [ \cfrac{17}{3} \right ]
A.6. x - \cfrac{1}{5}=\cfrac{2}{3} \left [ \cfrac{13}{15} \right ]
A.7. x + \cfrac{1}{2}=-\cfrac{3}{2} \left [-2]

In questi esercizi bisogna sommare i coefficienti che moltiplicano la x e poi operare come negli esercizi precedenti.

B.1.  \cfrac{1}{2}x+\cfrac{1}{2}x+\cfrac{5}{6}=\cfrac{8}{6}  \left [1]
B.2. \cfrac{1}{3}x+\cfrac{2}{3}x-\cfrac{1}{4}=\cfrac{3}{4}  \left [ 1 ]
B.3. \cfrac{5}{6}x+\cfrac{1}{6}x-\cfrac{1}{5}=\cfrac{4}{5}  \left [1]
B.4. \cfrac{1}{4}x+\cfrac{3}{4}x-\cfrac{3}{2}=\cfrac{5}{2}  \left [4]
B.5. \cfrac{2}{5}x+\cfrac{3}{5}x-\cfrac{7}{3}=\cfrac{10}{3}  \left [ \cfrac{17}{3} \right ]
B.6. \cfrac{1}{5}x+\cfrac{4}{5}x-\cfrac{1}{5}=\cfrac{2}{3}  \left [ \cfrac{13}{15} \right ]
B.7. \cfrac{4}{7}x+\cfrac{3}{7}x-\cfrac{1}{2}=\cfrac{3}{2}   \left [2]

Negli esercizi successivi, il numero che moltiplica la x deve essere diviso da entrambe le parti ma, essendoci una frazione, è molto più semplice moltiplicare a destra e a sinistra per la frazione che ha come denominatore il numero che moltiplica la x.

Ad esempio

2x=\cfrac{1}{3}

La prima cosa che viene da fare è il seguente passaggio:

\cfrac{2x}{2}=\cfrac{\cfrac{1}{3}}{2}

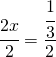
ma la cosa che ritengo più semplice è invece questa:

\cfrac{1}{2}\cdot 2x=\cfrac{1}{3}\cdot \cfrac{1}{2}

\cfrac{1}{\not 2}\cdot \not 2x=\cfrac{1}{6}

x=\cfrac{1}{6}

Seguendo l’esempio precedente, risolvere questi esercizi

C.1. 3x=\cfrac{1}{4}
C.2. 4x=\cfrac{1}{5}
C.3. 5x=\cfrac{1}{6}
C.4. 6x=\cfrac{1}{7}
C.5. 7x=\cfrac{1}{8}
C.6. 8x=\cfrac{1}{9}
C.7. 9x=\cfrac{1}{10}
C.8. 4x=\cfrac{2}{3}
C.9. 6x=\cfrac{2}{5}
C.10. 7x=\cfrac{14}{5}
C.11. 8x=\cfrac{16}{3}
C.12. 9x=\cfrac{18}{5}
C.13. 10x=\cfrac{20}{3}

Negli esercizi successivi il numero che moltiplica la x è una frazione.

Ad esempio:

\cfrac{1}{2}x=\cfrac{1}{4}

In questo caso moltiplico a sinistra ed a destra per il denominatore della frazione che moltiplica la x

2\cdot \cfrac{1}{2}x=\cfrac{1}{4}\cdot 2

\not 2\cdot \cfrac{1}{\not 2}x=\cfrac{1}{4}\cdot 2

x=\cfrac{1}{2\cdot 2}\cdot 2

x=\cfrac{1}{2\cdot \not 2}\cdot \not 2

x=\cfrac{1}{2}

Seguendo l’esempio precedente,  risolvere questi esercizi:

D.1. \cfrac{1}{3}x=\cfrac{1}{4}
D.2. \cfrac{1}{4}x=\cfrac{1}{5}
D.3. \cfrac{1}{5}x=\cfrac{1}{6}
D.4. \cfrac{1}{6}x=\cfrac{1}{7}
D.5. \cfrac{1}{7}x=\cfrac{1}{8}
D.6. \cfrac{1}{8}x=\cfrac{1}{9}
D.7. \cfrac{1}{9}x=\cfrac{1}{10}
D.8. \cfrac{1}{4}x=\cfrac{2}{3}
D.9. \cfrac{1}{6}x=\cfrac{2}{5}
D.10. \cfrac{1}{7}x=\cfrac{14}{5}
D.11. \cfrac{1}{8}x=\cfrac{16}{3}
D.12. \cfrac{1}{9}x=\cfrac{18}{5}
D.13. \cfrac{1}{10}x=\cfrac{20}{3}

Adesso è necessario fondere gli esercizi del gruppo C con quelli del gruppo D per risolvere gli esercizi successivi.

Ad esempio:

\cfrac{3}{4}x=\cfrac{5}{7}

moltiplico a sinistra e a destra per il reciproco del numero che moltiplica la x ossia:

\cfrac{4}{3}\cdot \cfrac{3}{4}x=\cfrac{5}{7}\cdot \cfrac{4}{3}

\cfrac{\not 4}{\not 3}\cdot \cfrac{\not 3}{\not 4}x=\cfrac{5}{7}\cdot \cfrac{4}{3}

x=\cfrac{20}{21}

Seguendo l’esempio precedente,  risolvere questi esercizi:

CD.1. \cfrac{4}{5}x=\cfrac{6}{7}  \left [ \cfrac{15}{14} \right ]
CD.2. \cfrac{5}{6}x=\cfrac{7}{8}  \left [ \cfrac{21}{20} \right ]
CD.3. \cfrac{6}{7}x=\cfrac{8}{9}  \left [ \cfrac{28}{27} \right ]
CD.4. \cfrac{7}{8}x=\cfrac{9}{10}  \left [ \cfrac{36}{35} \right ]
CD.5. \cfrac{8}{9}x=\cfrac{10}{11}  \left [ \cfrac{45}{44} \right ]
CD.6. \cfrac{9}{10}x=\cfrac{4}{5}  \left [ \cfrac{8}{9} \right ]
CD.7. \cfrac{6}{5}x=\cfrac{8}{7}  \left [ \cfrac{20}{21} \right ]
CD.8. \cfrac{7}{6}x=\cfrac{9}{8}  \left [ \cfrac{27}{28} \right ]

Se si sono risolti gli esercizi precedenti con sicurezza, si possono affrontare questi esercizi.

Per un livello sufficiente [6]:

6.1. x+\cfrac{1}{2}=-\cfrac{3}{2} \left [ -2 \right ]
6.2. \cfrac{2}{3}-x=\cfrac{1}{3} \left [ \cfrac{1}{3} \right ]
6.3. -\cfrac{5}{2}x+\cfrac{1}{3}=-\cfrac{3}{2}x+\cfrac{4}{3} \left [ -1 \right ]
6.4. \cfrac{2}{5}x-3=-\cfrac{3}{5}x+6 \left [ 9 \right ]
6.5. \cfrac{1}{2}x+2x+\cfrac{4}{3}=\cfrac{1}{12}+2x \left [-\cfrac{5}{2} \right ]
6.6. \cfrac{2}{5}x-\cfrac{3}{5}-\cfrac{1}{3}x=1+\cfrac{1}{5}x-\cfrac{1}{3}-\cfrac{1}{15} \left [-9 \right ]
6.7. \cfrac{1}{2}+\cfrac{5}{4}x-\cfrac{1}{8}x+\cfrac{1}{4}=\cfrac{3}{16}x-\cfrac{1}{2} \left [- \cfrac{4}{3} \right ]

Esercizi per il [7]

7.1. 2x+\cfrac{17-x}{2}=\cfrac{8-3x}{3}+\cfrac{25}{3} \left [ 1 \right ]
7.2. x-1-\cfrac{x+3}{2}-3=\cfrac{1-x}{3} \left [ 7 \right ]
7.3. \cfrac{x}{2}+3=5-x \left [- \cfrac{4}{3} \right ]

 [:en]

Pablo Picasso

Pablo Picasso

1) x + \cfrac{1}{2}=-\cfrac{3}{2}

2) \cfrac{2}{3}-x=\cfrac{1}{3}

3) -\cfrac{5}{2}x+\cfrac{1}{3}=-\cfrac{3}{2}x+\cfrac{4}{3}

4) \cfrac{2}{5}x-3=-\cfrac{3}{5}x+6

5) \cfrac{1}{2}x+2x+\cfrac{4}{3}=\cfrac{1}{12}+2x

__________________________________________

6) \cfrac{2}{5}x-\cfrac{3}{5}-\cfrac{1}{3}x=1+\cfrac{1}{5}x-\cfrac{1}{3}-\cfrac{1}{15}

7) \cfrac{1}{2}+\cfrac{5}{4}x-\cfrac{1}{8}x+\cfrac{1}{4}=\cfrac{3}{16}x-\cfrac{1}{2}

9) \cfrac{2}{3}x-1+\cfrac{x}{6}=15-x-\cfrac{x}{6}

10) \cfrac{1}{2}x-1+2x-3+4x-5=1-\cfrac{1}{2}x

11) \cfrac{1}{2}x+3+\cfrac{1+x}{3}=7-x

12) x-1-\cfrac{x+3}{2}-3=\cfrac{1-x}{3}

13) \cfrac{x}{2}+3=5-x

14) 5x-1=7-\cfrac{x}{3}

15) \cfrac{x}{3}-2=\cfrac{5}{3}+x

16) \cfrac{x}{5}+2=\cfrac{1}{5}-x[:de]

Pablo Picasso

Pablo Picasso

1) x + \cfrac{1}{2}=-\cfrac{3}{2}

2) \cfrac{2}{3}-x=\cfrac{1}{3}

3) -\cfrac{5}{2}x+\cfrac{1}{3}=-\cfrac{3}{2}x+\cfrac{4}{3}

4) \cfrac{2}{5}x-3=-\cfrac{3}{5}x+6

5) \cfrac{1}{2}x+2x+\cfrac{4}{3}=\cfrac{1}{12}+2x

__________________________________________

6) \cfrac{2}{5}x-\cfrac{3}{5}-\cfrac{1}{3}x=1+\cfrac{1}{5}x-\cfrac{1}{3}-\cfrac{1}{15}

7) \cfrac{1}{2}+\cfrac{5}{4}x-\cfrac{1}{8}x+\cfrac{1}{4}=\cfrac{3}{16}x-\cfrac{1}{2}

9) \cfrac{2}{3}x-1+\cfrac{x}{6}=15-x-\cfrac{x}{6}

10) \cfrac{1}{2}x-1+2x-3+4x-5=1-\cfrac{1}{2}x

11) \cfrac{1}{2}x+3+\cfrac{1+x}{3}=7-x

12) x-1-\cfrac{x+3}{2}-3=\cfrac{1-x}{3}

13) \cfrac{x}{2}+3=5-x

14) 5x-1=7-\cfrac{x}{3}

15) \cfrac{x}{3}-2=\cfrac{5}{3}+x

16) \cfrac{x}{5}+2=\cfrac{1}{5}-x[:]

Questa voce è stata pubblicata in Senza categoria. Contrassegna il permalink.

53 risposte a Equazioni di primo grado a coefficienti frazionari

  1. Valentina Cipriani scrive:
    11 Settembre 2015 alle 09:45

    🙂

    Rispondi
  2. francesko cela scrive:
    11 Settembre 2015 alle 09:46

    buona giornata profeeee

    Rispondi
  3. Denise Cerizza scrive:
    11 Settembre 2015 alle 09:47

    ciao

    Rispondi
  4. samuel folie scrive:
    11 Settembre 2015 alle 09:47

    salve prof

    Rispondi
  5. Sophia Albertoni Rovai scrive:
    11 Settembre 2015 alle 09:47

    salve 🙂

    Rispondi
  6. Ervin Gjeka scrive:
    11 Settembre 2015 alle 09:48

    Salve prof. Bragadin

    Rispondi
  7. Maikol Rizzi scrive:
    11 Settembre 2015 alle 09:48

    Salve Prof. Bragadin

    Rispondi
  8. lorenzo scrive:
    11 Settembre 2015 alle 09:49

    bella prof 😛

    Rispondi
  9. francesco scrive:
    11 Settembre 2015 alle 09:49

    Buongiorno prof.

    Rispondi
  10. Pietro scrive:
    11 Settembre 2015 alle 09:50

    Salve Profe Zlatan

    Rispondi
  12. Davide Polli scrive:
    11 Settembre 2015 alle 09:52

    Salve Prof. Bragadin

    Rispondi
  13. ayoub scrive:
    11 Settembre 2015 alle 09:52

    Buon pranzo

    Rispondi
  14. Marco Amenici scrive:
    11 Settembre 2015 alle 09:53

    ciaoo Raga, davvero belli sti esercizzi 😉

    Rispondi
  15. Maikol Rizzi scrive:
    11 Settembre 2015 alle 09:53

    la prima è uscita x=-2/1

    Rispondi
  16. Valentina Cipriani scrive:
    11 Settembre 2015 alle 09:54

    a me la prima risulta -2

    Rispondi
  17. Davide Polli scrive:
    11 Settembre 2015 alle 09:55

    1) x= -2

    2)x=1/3

    Rispondi
  18. mathew baroi scrive:
    11 Settembre 2015 alle 09:59

    conincio subito prof.

    Rispondi
  19. Davide Polli scrive:
    11 Settembre 2015 alle 10:03

    3)X= -1
    4)X=9

    Rispondi
  20. Valentina Cipriani scrive:
    11 Settembre 2015 alle 10:04

    2) X=1/3

    Rispondi
  21. Francesco Bragadin scrive:
    11 Settembre 2015 alle 10:04

    Bravi Davide e Valentina

    Rispondi
  22. Davide Polli scrive:
    11 Settembre 2015 alle 10:06

    5)X=-15/6

    Rispondi
  23. Davide Polli scrive:
    11 Settembre 2015 alle 10:10

    6)X=-8

    Rispondi
  24. mathew baroi scrive:
    11 Settembre 2015 alle 10:13

    fatto i primi due

    Rispondi
  25. samuel folie scrive:
    11 Settembre 2015 alle 10:15

    1) x=-2
    2)x=1/3
    3)x=3
    4)x=9
    5)x=-15/6

    Rispondi
  26. Valentina Cipriani scrive:
    11 Settembre 2015 alle 10:16

    3)X=1

    Rispondi
  27. Davide Polli scrive:
    11 Settembre 2015 alle 10:18

    7)X=-1/15

    Rispondi
  28. samuel folie scrive:
    11 Settembre 2015 alle 10:18

    6)x=-8

    Rispondi
  29. Kinza Latif scrive:
    6 Dicembre 2016 alle 08:22

    CD
    1) x= 15/14
    2) x= 21/20
    3) x= 28/27
    4) x= 36/35
    5) x= 45/44
    6) x= 8/9
    7) x= 20/21
    8) x= 27/28

    Rispondi
  30. Luca Bagnoli scrive:
    14 Dicembre 2016 alle 10:27

    grande profeeeee

    Rispondi
  31. Lidian Hidri scrive:
    14 Dicembre 2016 alle 10:30

    B.7. (2)

    Rispondi

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *