6.1.

![]()
Raccolgo le x a sinistra del verso della disequazione e i numeri a destra.
Per fare questo sommo a sinistra e destra
- -7
- -2x
![]() .
.
![]() .
.
![]() .
.
![]()
Vale sempre il fatto che il numero che moltiplica la x debba essere l’1 per cui divido a destra e a sinistra per 2
![]()
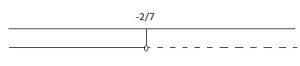
la soluzione è:
![]()
Bisogna sempre fare la rappresentazione grafica della soluzione:
 6.2.
6.2.
![]() .
.
![]() .
.
![]() .
.
Siccome il coefficiente della x è negativo cambio di segno moltiplicando per -1 a sinistra e a destra e cambio il verso della disequazione.
![]() .
.
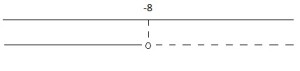
![]() .
.
![]()
7.1.
Primo metodo
![]()
in questo semplice caso si potrebbe direttamente raggruppare le x a sinistra del verso e i numeri a destra:
![]()
![]()
cambio il verso della disequazione:
![]()
quindi divido a sinistra e a destra per 3 ed ho:
![]()
![]()
![]()
Secondo metodo
![]()
Faccio il minimo comune multiplo a sinistra e a destra:
![]()
moltiplico per 2 a sinistra e a destra:
![]()
![]()
![]()
![]()
moltiplico per -1 a sinistra e a destra cambiando il verso della disequazione
![]()
![]()
![]()
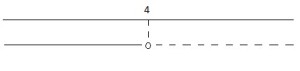
e quindi
![]()
Graficamente è:
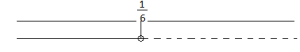 7.2.
7.2.
![]()
minimo comune multiplo
![]()
![]()
![]()
![]()
![]()
![]()
la soluzione è:
![]()
Graficamente
 8.1.
8.1.
![]()
Per essere in grado di affrontare agevolmente questa è necessario ricordarsi bene i prodotti notevoli.
La prima parentesi è il quadrato della differenza di un binomio, mentre l’ultima parentesi e la differenza del quadrato di un binomio.
![]()
Si noti come l’ultima parentesi l’ho tenuta in quanto vi è il simbolo – che modifica il segno di tutti i monomi presenti all’interno della parentesi.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
e la soluzione diventa:
![]()
Graficamente si ha: