[:it]Per esercitarsi sulla definizione di potenza
Esercizi di base.
Calcolare il valore delle seguenti potenze:
| B.1. |
|
| B.2. |
|
| B.3. |
|
| B.4. |
|
| B.5. |
|
| B.6. |
Scrivere i seguenti numeri sotto forma di potenza effettuando la scomposizione, (tale argomento viene trattato in maniera esaustiva anche nel post relativo al calcolo del m.c.m. o M.C.D.)
| B.7. 100 | |
| B.8. 27 | |
| B.9. 32 | |
| B.10. 125 | |
| B.11. 64 | |
| B.12. 243 | |
| B.13. 121 |
Applicando la proporietà commutativa del prodotto (ossia che invertendo i membri il risultato non cambia, ad esempio ![]() scrivere i seguenti prodotti utilizzando le potenze:
scrivere i seguenti prodotti utilizzando le potenze:
| B14. |
|
| B15. |
|
| B16. |
|
| B.17. |
Risolvere i seguenti esercizi applicando, in ogni caso, la proprietà relativa. Indicare i risultati sotto forma di potenza.
| B18. |
|
| B19. |
|
| B20. |
|
| B21. |
Applicando le proprietà delle potenze, se è possibile, calcolare le seguenti espressioni.
Esercizi per un livello sufficiente [6]:
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
|
| 6.5. |
|
| 6.6. |
|
| 6.7. |
|
| 6.8. |
|
| 6.9. |
|
| 6.10. |
|
| 6.11. |
Esercizi per un livello discreto [7]:
| 7.1. |
|
| 7.2. |
|
| 7.3. |
|
| 7.4. |
|
| 7.5. |
|
| 7.6. |
|
| 7.7. |
Esercizi per un buon livello [8]
| 8.1. |
|
| 8.2. |
Esercizi per un ottimo livello [9/10]
| 9.1. |
|
| 9.2. |
Soluzioni[:]

Il risultato è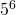
6.6 Il risultato è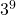
Concordo
anch’io
Fate attenzione alla 7.1. bisogna scomporre il 12 nei sui fattori, non necessariamente primi. Ossia, solo, per questo esempio, il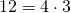
6.7 Il risultato è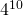
Il risultato non è corretto prova a rivedere i calcoli soprattutto, secondo me la seconda parte
il risultato è
6.5 il risultato è 5^6
oppure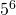
Brava adesso prova anche le altre
6.6 il risultato è 3^9