[:it]
Ogni numero deve essere pensato con il suo segno ossia + o -.
Tale notazione ha numerose applicazioni:
- la misurazione della temperatura: possiamo essere sopra o sotto lo zero dove lo zero indica per convenzione la temperatura di solidificazione dell’acqua
- il movimento di capitali
- periodi di tempo rispetto ad un tempo prefissato: si pensi prima e dopo la nascita di Cristo
- rispetto ad un prefissato meridiano ci si può trovare da una parte o dall’altra
- sopra o sotto il livello del mare
Come si effettuano le operazioni con i numeri relativi.
S O M M A
Se i due numeri hanno lo stesso segno si sommano le cifre e si prende il segno uguale
es: -8 -2 = – 10 ossia prendo 8 + 2 = 10 e metto il segno comune ossia il – ed appunto -10
Se i due numeri hanno segno opposto prendo il più grande e vi sottraggo il più piccolo prendendo sempre il segno del più grande
esempio
-8 + 2
- prendo 8 e sottraggo il 2: 8 – 2 = 6
- prendo il segno della cifra più grande (è l’8) ossia il – e lo metto davanti al risultato
- il risultato è -6
esempio
+10 -2
- prendo 10 e sottraggo il 2: 10 – 2 = 8
- prendo il segno della cifra più grande (è il 10) ossia il + e lo metto davanti al risultato
- il risultato è +8
M O L T I P L I C A Z I O N E / D I V I S I O N E
Bisogna ricordarsi la seguente regola:
![]()
![]()
![]()
![]()
Prima si stabilisce il segno risultante della moltiplicazione seguendo la tabella precedente e poi si esegue la normale moltiplicazione tra le cifre
esempio
![]()
- prima il segno risultante è + perché
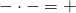
- moltiplico le cifre
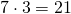
- metto davanti al risultato il segno determinato dal primo passo
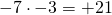
esempio
![]()
- prima il segno risultante è – perché
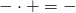
- moltiplico le cifre
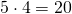
- metto davanti al risultato il segno determinato dal primo passo
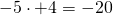
esempio
![]()
- prima il segno risultante è – perché
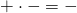
- moltiplico le cifre
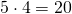
- metto davanti al risultato il segno determinato dal primo passo
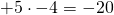
esempio
![]()
- prima il segno risultante è + perché
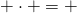
- moltiplico le cifre
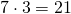
- metto davanti al risultato il segno determinato dal primo passo
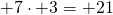
CONFRONTO TRA NUMERI RELATIVI
Per valutare che un numero relativo sia più grande di un altro si deve confrontare il segno; se segni opposti il numero con il segno negativo è sempre minore; se di segno uguale si hanno due casi:
- se entrambi negativi il numero più piccolo è quello con la parte unitaria più grande
- se entrami positivi il numero più piccolo è quello con la parte unitaria più piccola.
ATTENZIONE
Il segno minore è <
il segno maggiore è >
[:]

