[:it] Sommare numeri relativi frazionari dignifica applicare comunque tutto ciò che si è appreso con la somma delle frazioni.
Sommare numeri relativi frazionari dignifica applicare comunque tutto ciò che si è appreso con la somma delle frazioni.
Lo richiamo qui con un esempio perché tutta la teoria è presente nel post:
Allora:
![]()
Esercizi suddivisi per un livello sufficiente [6]:
| 6.1. (+3)+(-5)+(-6) | [-8] |
| 6.2. (+8) + (-10)+(+11) | [+9] |
| 6.3. (-1)+(-3)+(-7) | [-11] |
| 6.4. (-2)+(+7)+(-8) | [-3] |
6.5. 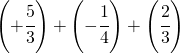 |
|
6.6. 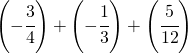 |
|
6.7. 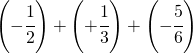 |
[ -1 ] |
6.8. 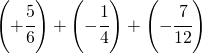 |
[ 0] |
6.9. 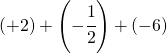 |
|
6.10. 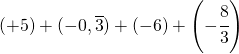 |
|
6.11. 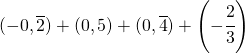 |
|
6.12. 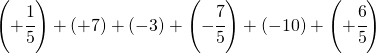 |
[-6] |
6.13. 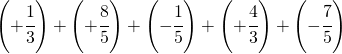 |
|
6.14. 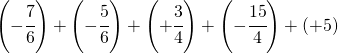 |
[0] |
| 6.15. (+13)+(+32)+(-5)+(-7)+(-10)+(+7) | [+30] |
| 6.16. (-25)+(-10)+(+8)+(+2)+(+4)+(+13) | [-8] |
| 6.17. (15-9)+(11+4-28-9)+(-8+16-11) | [-19] |
6.18. 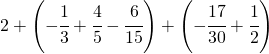 |
[+2] |
Si devono eseguire le operazioni a partire da quelle contenute nelle parentesi più interne
Esercizi per un livello discreto [7]:
7.1. 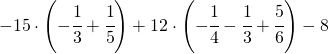 |
[-3] |
7.2. 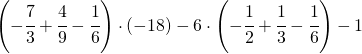 |
[+38] |
7.3. 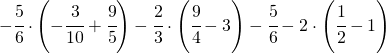 |
|
7.4. 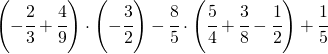 |
|
7.5. 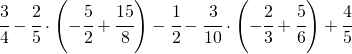 |
Esercizi per un buon livello [8]
8.1. 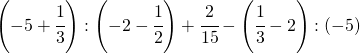 |
|
8.2. 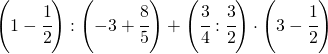 |
|
8.3. 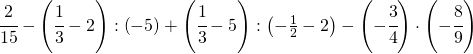 |
[+1] |
Esercizi per un ottimo livello [9/10]
10.1. 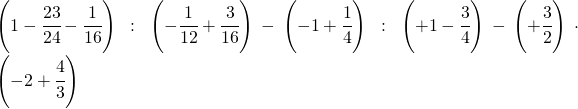 |

6.6= 8/12
6.7= 4/6
6.8= 0/12
6.9= 14/12
Il risultato della 7.5 è 5/4 non 4/5