[:it]Integrali: calcolo delle aree. Problema 1[:]

[:it]

Francis Picabia

Rappresenta graficamente 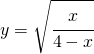$y=\sqrt{\cfrac{x}{4-x}}$ e determina l’area della regione di piano compresa fra la curva, l’asse delle y e la retta tangente alla curva nel suo punto di flesso. (suggerimento. Per il calcolo dell’integrale poni $x=4\sin ^{2}t$ ).

Sviluppo.
Intanto rappresento graficamente la curva.
Per calcolare il dominio si deve porre l’argomento della radice $\geqslant 0$ ed il denominatore $\neq 0$ .
$\cfrac{x}{4-x}\geqslant 0$
Il numeratore è positivo per
$x\geqslant 0$
il denominatore non può essere negativo per cui ho:
$4-x> 0$
ossia
$x<4$
unendo le due disequazioni e valutando il segno si ha:

Rendered by QuickLaTeX.com

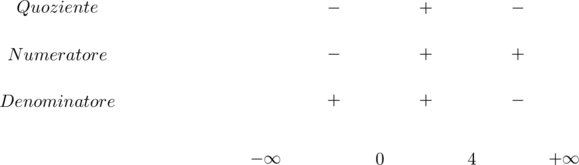
Quindi il dominio è:
$D=\left \{ \forall x\in \mathbb{R}| 0\leqslant x<4 \right \}$

Presenta un asintoto verticale in $x=4$ e, sempre usando lo studio del segno della funzione:
$\underset{x\rightarrow 4^{-}}{lim}\sqrt{\cfrac{x}{4-x}}=+\infty$

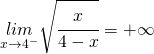
Adesso bisogna fare la derivata prima e successivamente la derivata seconda per determinare il punto di flesso e l’equazione della retta in esso tangente.
$y'=\cfrac{1}{2\sqrt{\cfrac{x}{4-x}}}\cdot \cfrac{\left ( 4-x \right )-x\left ( -1 \right )}{\left ( 4-x \right )^{2}}$
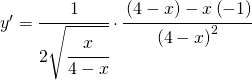
semplificandola opportunamente si ha:
$y'=\cfrac{2}{\sqrt{\cfrac{x}{4-x} }\cdot \left ( 4-x \right )^{2}}$
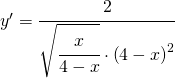
per trovare il flesso devo calcolare la derivata seconda.

Per comodità riscrivo la derivata prima nella seguente maniera:

$y'=2\left ( \cfrac{x}{4-x} \right )^{-\frac{1}{2}}\cdot \left ( 4-x \right )^{-2}$
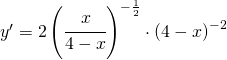
la derivata seconda deve essere posta a zero per trovare il punto di flesso.
$y^{''}=2\left ( -\cfrac{1}{2} \right )\left ( \cfrac{x}{4-x} \right )^{-\frac{3}{2}}\cfrac{4}{\left ( 4-x \right )^{2}}\left ( 4-x \right )^{-2}+2\left ( \cfrac{x}{4-x} \right )^{-\frac{1}{2}}(-2)\left ( 4-x \right )^{-3}(-1)$

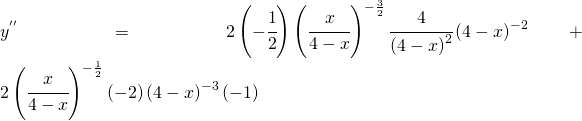
semplificandola in maniera opportuna essa diventa:
$y^{''}=-\cfrac{1}{x\sqrt{\cfrac{x}{4-x}}}+\cfrac{1}{\sqrt{\cfrac{x}{4-x}}}$

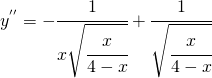
che si annulla per $x=1$

Sostituendo il valore trovato alla funzione di partenza 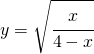$y=\sqrt{\cfrac{x}{4-x}}$
$F_{y}=\cfrac{1}{\sqrt{3}}$
Le coordinate del punto di flesso sono:
$F\left ( 1;\cfrac{1}{\sqrt{3}} \right )$

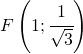
per trovare il coefficiente angolare della retta passante per il punto di flesso è sufficiente calcolare il valore della derivata prima in $x=1$
$y^{'}(1)=\cfrac{1}{\cfrac{1}{\sqrt{3}}}\cdot \cfrac{2}{9}$
$m=\cfrac{2}{9}\sqrt{3}$
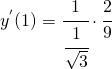
La retta tangente alla curva e passante per il punto di flesso ha equazione:
$y-\cfrac{1}{\sqrt{3}}=\cfrac{2}{9}\sqrt{3}\left ( x-1 \right )$
Rappresento sul piano cartesiano la curva e la retta.

Rendered by QuickLaTeX.com

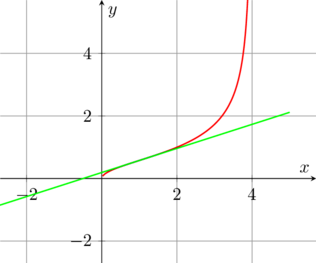
Per meglio capire la zona di cui si deve calcolare l’area evidenzio solo la zona di interesse ossia per $0<x<1$

Rendered by QuickLaTeX.com

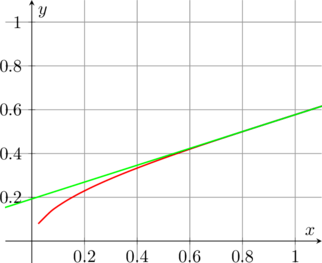
L’area voluta è quel piccolo spicchio tra l’asse y la retta e la curva per cui si dovranno calcolare i seguenti integrali:

(1) $\begin{equation*} A=\int_{0}^{1}\cfrac{2}{9}\sqrt{3}x+\cfrac{\sqrt{3}}{9}\, dx-\int_{0}^{1}\sqrt{\cfrac{x}{4-x}}\, dx \end{equation*}$

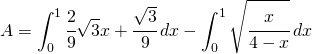
Il primo integrale è facilmente risolvibile

(2) $\begin{equation*} \left.\begin{matrix} \cfrac{2}{9}\sqrt{3}\cdot \cfrac{x^{2}}{2}+\cfrac{\sqrt{3}}{9}\cdot x \end{matrix}\right|_{0}^{1}=\cfrac{\sqrt{3}}{9}+ \cfrac{\sqrt{3}}{9}=\cfrac{2}{9}\cdot \sqrt{3} \end{equation*}$

La seconda parte dell’integrale chiede la seguente sostituzione $x=4\sin ^{2}t$ , derivando

$dx=8\sin t\cos t\,dt$

cambiando gli estremi di integrazione, in seguito alla sostituzione:

$4\sin ^{2}t=0$
risolta dà
$t=0$
e
$4\sin ^{2}t=1$
$\sin ^{2}t=\cfrac{1}{4}$
prendo solo la radice positiva
$\sin t=\cfrac{1}{2}$
$t=\cfrac{\pi}{6}$

diventa:

(3) $\begin{equation*} \int_{0}^{\frac{\pi}{6}}\sqrt{\cfrac{4\sin ^{2}t}{4-4\sin ^{2}t}}\cdot 8\sin t\cos t\,dt \end{equation*}$

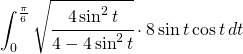
ricordandosi l’equazione goniometrica:

$\sin ^{2}t+\cos ^{2}t=1$ ed applicandola al denominatore della (3)
$4-4\sin ^{2}t=4\left ( 1-\sin ^{2}t \right )=4\cos ^{2}t$

la (3) diventa:

(4) $\begin{equation*} \int_{0}^{\frac{\pi }{6}}\sqrt{\cfrac{4\sin^{2}t}{4\cos^{2}t}}\cdot 8\sin t\cos t\,dt=\int_{0}^{\frac{\pi }{6}}\cfrac{\sin t}{\cos t}\cdot 8\sin t\cos t\,dt=8\int_{0}^{\frac{\pi }{6}}\sin^{2} t\,dt \end{equation*}$

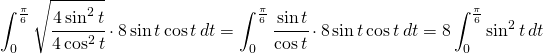
La primitiva si può calcolare attraverso l’integrazione per parti.
$\int \sin ^{2}t\, dt=\int \sin t \cdot \sin t \, dt=-\sin t\cos t+\int \cos ^{2}t \, dt$
utilizzando sempre l’equazione goniometrica
$\int \sin ^{2}t\, dt= -\sin t\cos t+\int 1-\sin ^{2}t \, dt=-\sin t\cos t+t -\int \sin ^{2}t \, dt$
spostando al primo membro i due integrali si ha:
$2\int \sin ^{2}t\, dt= -\sin t\cos t+t$
e l’integrale risolto diventa:
$\int \sin ^{2}t\, dt= -\cfrac{1}{2}\sin t\cos t+\cfrac{1}{2}t$

(5) $\begin{equation*} 8\int_{0}^{\frac{\pi }{6}}\sin^{2} t\,dt\left=\begin{matrix} -4\sin t\cos t+4t\end{matrix}\right|_{0}^{\frac{\pi}{6}}=-\sqrt{3}+\cfrac{2}{3}\pi \end{equation*}$

Adesso sottraendo alla (2) la (5) si ha il risultato:

$\cfrac{2}{9}\sqrt{3}+\sqrt{3}-\cfrac{2}{3}\pi =\cfrac{11}{9}\sqrt{3}-\cfrac{2}{3}\pi$

[Questo post è interamente scritto in LaTex]

[:]

Lascia un commento Annulla risposta

Registrazione

Categorie

Articoli recenti

Commenti recenti

Meta

Categorie

Articoli recenti

Commenti recenti

Meta

Whymatematica