[:it]
500-esimo post
L’equazione di una sfera è:
le coordinate del centro sono:
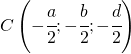
il raggio sarà:
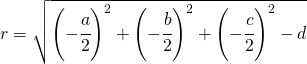
oppure essa può essere vista come
Ad esempio questo è il grafico della sfera di equazione:
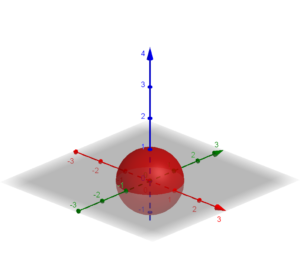
I problemi che si incontrano sono i seguenti:
- intersezione di un piano con una sfera
- intersezione di una retta nello spazio con una sfera.
INTERSEZIONE PIANO E SFERA
Un piano ed una sfera possono:
- non incontrarsi
- incontrarsi
- si identifica un punto
- si identifica una circonferenza
- di questa circonferenza calcolare il centro ed il raggio ossia la sua equazione
Condizione di intersezione è che la distanza dal centro ed il piano siano minori o uguali al raggio della sfera.
Un piano ha equazione:
Calcolo la distanza di un punto da un piano utilizzando la seguente formula:
se 
allora ho la condizione di tangenza o secante.
Per determinare il raggio della circonferenza identificata dall’intersezione del piano con la sfera è si è in questa situazione:
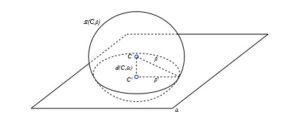
il raggio della circonferenza si calcola applicando il teorema di Pitagora applicato al triangolo rettangolo che ha:
base il raggio della circonferenza
altezza la distanza tra il centro della sfera e il centro della circonferenza
ipotenusa il raggio della sfera
Per calcolare il centro della circonferenza, si deve calcolare la retta passante per un punto nello spazio e perpendicolare al piano che interseca la sfera.
Per vedere un’applicazione la cosa migliore è vedere un esempio che esplicita tutti i passaggi necessari[:]