[:it]

Guido Borelli
Normalmente una retta viene sempre definita nella forma
![]()
o nella forma
![]()
che viene utilizzata solo quando si deve determinare la distanza tra un punto ed una retta.
Che significato hanno ![]() e
e ![]() ?
?
Essi rappresentano proprio le componenti del vettore ![]() perpendicolare alla retta.
perpendicolare alla retta.
Graficamente si vede benissimo tale fatto.
La retta ![]()
ha vettore ![]()

Date due rette
![]()
![]()
Condizione di parallelismo
Saranno parallele quando i due vettori saranno una combinazione lineare dell’uno rispetto all’altro quindi:
![]()
![]()
o meglio:
![]()
graficamente si vede la cosa:
date le rette
![]()
![]()
sono parallele

e si vede che i due vettori sono sovrapposti ed uno è proprio multiplo dell’altro.
Condizione di perpendicolarità
In seguito alla definizione di prodotto scalare tra due vettori, saranno perpendicolari due rette se
![]()
Graficamente.
Se si hanno le due rette
![]() con
con ![]()
![]() con
con ![]()

Retta in forma parametrica
Tale rappresentazione utilizza il vettore direzione. Vi sono infinite rappresentazione della retta in forma parametrica perché sono infiniti i vettori che sono paralleli ad una retta.
Tale vettore si chiama vettore direzione.
Ad esempio:
![]()
il vettore direzione ha le coordinate che sono i coefficienti di t
![]()

E’ molto più agevole avere la retta in forma parametrica per farne il grafico.
E’ la rappresentazione parametrica della retta
![]()

Passaggio dalla forma parametrica alla forma implicita.
Si risolve il sistema in funzione di t e si confrontano i due valori di t trovati.
Ad esempio:
![]()
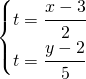
![]()
![]()
![]()
Passaggio dalla forma implicita alla forma parametrica
Vi sono vari metodi.
Uno è il seguente.
La forma implicita
![]()
fornisce il vettore ![]() , il vettore direzione è perpendicolare a questo per cui avrà coordinate
, il vettore direzione è perpendicolare a questo per cui avrà coordinate ![]()
La forma parametrica generale è:
![]()
dove v(l,m) è il vettore direzione e ![]() sono le coordinate di un punto appartenente alla retta.
sono le coordinate di un punto appartenente alla retta.
Ad esempio se ho la retta:
![]()
il vettore ![]() , il vettore direzione è
, il vettore direzione è ![]() ,
,
![]()
Adesso prendo il punto ![]() che appartiene alla retta.
che appartiene alla retta.
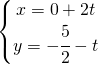 [:]
[:]
