[:it]Maturità 2017: terzo quesito[:]

Pubblicato il 26 Giugno 2017 da admin

[:it]

Paul Klee

Sapendo che:

(1)   \begin{equation*} \underset{x\rightarrow0}{lim}\cfrac{\sqrt{ax+2b}-6}{x}=1$ \end{equation*}

determinare i valori di a e b.

Prerequisiti

  • conoscere il calcolo con i limiti
  • sapere fare la razionalizzazione inversa
  • prodotto notevole della differenza del binomio
  • conoscere il metodo della fattorizzazione per eliminare gli zeri del numeratore e denominatore

Sviluppo

Sostituendo il valore 0 alla x del numeratore e del denominatore mi trovo nella situazione:

\cfrac{\sqrt{2b}-6}{0}=\infty

La razionalizzazione inversa è necessaria per poter semplificare la x presente al numeratore con quella del denominatore; utilizzo il prodotto notevole

(2)   \begin{equation*} \left ( a+b \right )\cdot \left ( a-b \right )=a^{2}-b^{2} \end{equation*}

Bisogna anche ricordarsi che il quadrato di una radice quadrata mi dà proprio il radicando ossia l’argomento della radice.

(3)   \begin{equation*} \left (\sqrt{5} \right )^2=5 \end{equation*}

Applicandola ad un prodotto notevole ho:

(4)   \begin{equation*} \left ( \sqrt{a}+b \right )\left ( \sqrt{a}-b \right )=\left ( \sqrt{a} \right )^2-b^{2}=a-b^2 \end{equation*}

Faccio la razionalizzazione inversa ossia moltiplico il numeratore ed il denominatore per \sqrt{ax+2b}+6 e la (1) diventa:

(5)   \begin{gather*} \cfrac{\left ( \sqrt{ax+2b}-6 \right )\left ( \sqrt{ax+2b}+6 \right )}{x\left ( \sqrt{ax+2b}+6 \right )} \\ \cfrac{ ax+2b-36 }{x\left ( \sqrt{ax+2b}+6 \right )} \end{gather*}

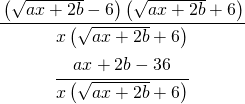
Adesso per togliere lo zero che annulla sia il numeratore che il denominatore pongo:

(6)   \begin{gather*} 2b-36=0 \\ b=18 \end{gather*}

sostituendo il valore trovato nella (6) nella (1) il limite diventa:

(7)   \begin{equation*} \underset{x\rightarrow0}{lim}\cfrac{ ax }{x\left ( \sqrt{ax+36}+6 \right )} \\ \end{equation*}

Solo adesso, dopo avere eseguito la razionalizzazione inversa, posso semplificare la x presente nel numeratore con quella del denominatore.

(8)   \begin{equation*} \underset{x\rightarrow0}{lim}\cfrac{ a }{\sqrt{ax+36}+6} \end{equation*}

Perché tale limite vada ad 1 è sufficiente risolvere la seguente equazione avendo posto a 0 il valore dell x (il valore a cui tende il limite)

(9)   \begin{gather*} \cfrac{ a }{\sqrt{36}+6}=1 \\ \cfrac{ a }{6+6}=1 \\ a=12 \end{gather*}

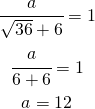
quindi ricapitolando i due valori sono:

(10)   \begin{gather*} a=12 \\ b=18 \end{gather*}

[:]

Questa voce è stata pubblicata in Senza categoria e contrassegnata con . Contrassegna il permalink.

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *