[:it]
Vladimir Kush
Un dado ha la forma di un dodecaedro regolare con le facce numerate da 1 a 12. Il dado è truccato in modo che la faccia contrassegnata dal numero 3 si presenti con una probabilità doppia rispetto a ciascun’altra faccia. Determinare il valore di 
in percentuale e calcolare la probabilità che in 5 lanci del dado la faccia 3 esca almeno 2 volte.
Prerequisiti
- conoscere i teoremi della probabilità
- conoscere la permutazioni con ripetizione
- conoscere la probabilità di eventi indipendenti
Sviluppo
La somma della probabilità di tutti gli eventi mi dà sempre 1.
Nel caso specifico la probabilità che esca la faccia dall’1 al 12 escluso il 3 è mentre 
se esce il 3; ho 11 facce equiprobabili, per cui vale la seguente equazione:
(1) 
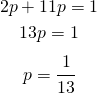
Perché un evento possa verificarsi almeno significa che potrebbe sempre capitare o esserci almeno il numero di volte richiesto.
Nel caso specifico la probabilità che in 5 lanci esca il 3 è dato da:
(2) 
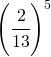
Per conoscere tutte le possibili permutazioni nel caso in cui uscisse 4 volte il 3 ed una sola volta un altro numero uso la seguente relazione:
(3) 
Si usa ad esempio quante parole diverse non di senso compito possono essere fatte con la parola AABCDE con il gruppo AA che si ripete.
Perché esca 4 volte
ho
(4) 
ad esempio 3 3 3 3 5
La probabilità diventa:
(5) 
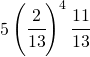
Perché esca 3 volte
ho
(6) 
ad esempio 3 3 3 5 5
La probabilità diventa:
(7) 
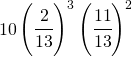
Perché esca 2 volte
ho
(8) 
ad esempio 3 3 5 5 5
La probabilità diventa:
(9) 
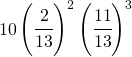
sommando la (2), (5), (7) e la (9) si ha
(10) 
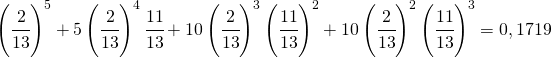
in percentuale diventa
il 17,19%[:]