[:it]

Vladimir Kush
Lo studio dei massimi e dei minimi per le funzioni a due variabili richiede l’introduzione di alcuni nuove strumenti matematici quali il gradiente e la matrice hessiana.
ll gradiente è un vettore le cui componenti sono le derivate parziali seconde della funzione, questo in un sistema ortonormale.
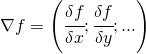
La matrice hessiana è composta dalle derivate seconde parziali opportunamente combinate, per semplicità scrivo quella relativa alla matrice quadrata di rango 2.
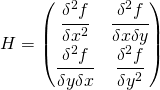
Per calcolare i massimi e i minimi di una funzione a più variabili attraverso la matrice hessiana devo analizzare le seguenti condizioni:
- annullare il gradiente
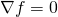 i relativi punti saranno poi usati nello studio del segno del determinante della matrice hessiana
i relativi punti saranno poi usati nello studio del segno del determinante della matrice hessiana 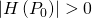 e
e 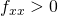 allora
allora 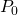 è un minimo relativo
è un minimo relativo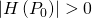 e e
e e 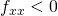 allora
allora 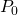 è un massimo relativo
è un massimo relativo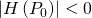 allora
allora 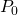 è un punto di sella.
è un punto di sella.
Con ![]()
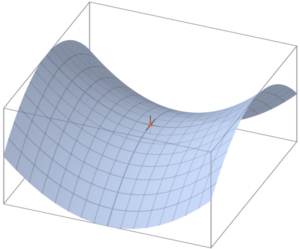
Il punto di sella è quel punto tale per cui la matrice hessiana rimane indefinita o in particolare è quel punto tale che prendendo due curve passanti per P esso è sia minimo che massimo graficamente si ha:
Moltiplicatori di Lagrange per la ricerca dei massimi e minimi vincolati
L’applicazione del teorema di Lagrange lo si usa quando la funzione è vincolata da un’altra. L’applicazione del teorema di Lagrange fornisce una condizione necessaria ma non sufficiente ma consente comunque la determinazione dei massimi e dei minimi vincolati.
Senza entrare nel formalismo del teorema è sufficiente sapere che data la funzione ![]() e la funzione vincolo
e la funzione vincolo ![]() si definisce
si definisce
![]()
Si annulla il gradiente di questa funzione e si sostituiscono i valori trovati in ![]() e li si confrontano e quelli minori sono i minimi e quelli maggiori sono i massimi.[:]
e li si confrontano e quelli minori sono i minimi e quelli maggiori sono i massimi.[:]
