[:it]
David Hettinger
Il codice di Hamming permette di correggere gli errori nella trasmissione inserendo della ridondanza nel codice trasmesso.
Nel caso specifico il codice di Hamming(7,4) inserisce in un codice di 4 bit, 3 bit in più appunto di ridondanza necessari per verificare e correggere il codice trasmesso.
In questo codice l’errore che si corregge è 1 di un bit e si parla quindi di distanza di Hamming di valore 1.
Al codice trasmesso si aggiungono dei bit di parità alla posizione 1, 2, 4, ricapitolando alla posizione:
Il bit 1 controlla la parità dei bit 1, 3, 5, 7
Il bit 2 controlla la parità dei bit 2, 3, 6, 7
Il bit 4 controlla la parità dei bit 4, 5,6, 7
Schematicamente ho quindi:
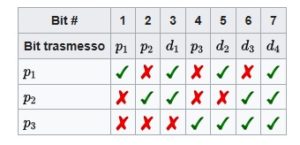Si nota che:
- il bit di parità 1 (p1) copre i bit 1 – 3- 5- 7
- il bit di parità 2 (p2) copre i bit 2 – 3- 6- 7
- il bit di parità 3 (p3) copre i bit 4 – 5 – 6- 7
Per leggere la tabella si deve andare a vedere la riga del Bit#
Il Bit 1 è controllato da p1
Il Bit 2 è controllato da p2
Il Bit 3 è controllato da p1 e p2
Il Bit 4 è controllato da p3
Il Bit 5 è controllato da p1 e p3
Il Bit 6 da p2 e p3
il Bit 7 da p1, p2 e p3.
In termini operativi si controllano p1, p2 e p3
| p1 | p2 | p3 |
| ok | ok | ok |
messaggio corretto
| p1 | p2 | p3 |
| no | ok | ok |
vedo che solo p1 è errato allora correggo il bit1
| p1 | p2 | p3 |
| no | ok | no |
p1 e p3 sono sbagliati.
ALGORITMO
Cerco la colonna con il segno di spunta verde su p1 e p3–> colonna 5 ossia relativa al Bit 4
Ossia partendo dalla riga con la spunta in verde si vede il relativo bit errato
Esempio:
Devo trasmetter 0101
il messaggio trasmesso sarà:
| P1 | P2 | M1 | P3 | M2 | M3 | M4 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
in quanto il P1 controlla la posizione 1357
P2 controlla la posizione 2367
P3controlla la posizione 4567
Mi arriva il seguente messaggio
| P1 | P2 | M1 | P3 | M2 | M3 | M4 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P1 è errato!
| P1 | P2 | M1 | P3 | M2 | M3 | M4 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P2 è errato!
| P1 | P2 | M1 | P3 | M2 | M3 | M4 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P3 è corretto.
Siccome P1 e P2 sono errati dalla tabella vedo che è errato il bit 3 e lo correggo da 1 a 0! Ed ho il messaggio di partenza corretto senza richiedere la ritrasmissione.
Il codice di Hamming(7,4) corregge solo 1 bit e si chiama appunto distanza 1. Non corregge gli errori doppi.[:]