TPSIT: applicazione teorema di Gauss

Campo elettrico di una lastra carica infinitamente estesa

$\phi =E\oint ds=E\cdot 2A$

con $A$ superficie della base della lastra.

$\phi =\cfrac{q}{\epsilon _{0}}$

per cui:

$\cfrac{q}{\epsilon _{0}}=2A\cdot E$

concludendo:

$E=\cfrac{\sigma }{2\epsilon _{0}}$

con $\sigma$ densità di carica superficiale.

Nel caso di un condensatore che è formato da due piastre caricate con cariche opposte il campo elettrico all’interno delle due piastre vale:

$E=\cfrac{\sigma }{\epsilon _{0}}$

il campo elettrico di un condensatore all’esterno è nullo in quanto i campi elettrici all’esterno si sottraggono mentre si sommano all’interno.

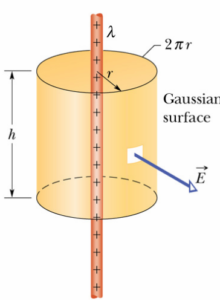Campo elettrico di un filo carico infinitamente lungo

$\phi =E\oint dS=E\cdot 2\pi rh$

con $2\pi r$ base del cilindro (filo) e $h$ lunghezza del filo.

$\phi =\cfrac{q}{\epsilon _{0}}$

unendo le due realzioni:

$\cfrac{q}{\epsilon _{0}}=E\cdot 2\pi rh$

da cui:

$E=\cfrac{\lambda }{2\pi \epsilon _{0}r}$ con

$\lambda =\cfrac{q}{h}$ densità lineare di carica.

Quindi il campo elettrico prodotto da un cavo diminuisce in maniera inversamente proporzionale alla distanza.

Nel caso in cui si inserisse un dielettrico aumenta il denominatore.

Questa voce è stata pubblicata in Senza categoria. Contrassegna il permalink.