[:it]

giacomo balla
Un campo magnetico variabile comporta l’esistenza di un campo elettrico e viceversa che un campo elettrico variabile comporta l’esistenza di un campo magnetico, e questo è una conseguenza del principio di relatività.
Le equazioni di Maxwell (alla base dell’elettromagnetismo) sono invarianti per le trasformazioni di Lorentz (sistema di riferimento relativistico), mentre non lo sono per quelle di Galileo.
Nel post che mette in relazione il potenziale elettrico con il campo elettrico, si era arrivati ad affermare che:
![]()
ossia:
![]()
inoltre il flusso di campo magnetico è dato da:
![]()
adesso unendo queste nella formula di Farady:
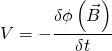
si ha:
![]()
In forma differenziale e lo inserisco solo per coerenza nella trattazione specifica la relazione precedente può essere scritta come:
![]()
che si legge il rotore di E è dato dalla variazione nel tempo del campo induzione magnetico.[:]
