1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
11) ![]()
12) ![]()

1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
11) ![]()
12) ![]()
a) Il perimetro di un trapezio isoscele è di 146cm e le basi sono rispettivamente di 26cm e 54cm. Calcola la misura di ciascun lato obliquo. [33cm]
b) In un trapezio isoscele, avente il perimetro di 155cm, ciascun lato obliquo è congruente alla base minore e l abase maggiore supera di 15 la base minore. Calcola la lunghezza di ciascun lato obliquo. [35cm]
c) Calcola il perimetro di un trapezio isoscele sapendo che ciascun lato obliquo misura 18cm, che la base minore è ![]() del lato obliquo e che la base maggiore è
del lato obliquo e che la base maggiore è ![]() della base minore. [68,4cm]
della base minore. [68,4cm]
d) Il perimetro di un triangolo isoscele è di 21,5 cm e la base minore misura 10,5cm. Calcola la misura dei lati obliqui del triangolo. [5,5cm]
e) Un triangolo equilatero, avente il lato di 25cm e un triangolo isoscele hanno lo stesso perimetro. Sapendo che la base del triangolo isoscele misura 31cm, calcola la misura dei due lati obliqui. [22cm]
f) Determina di quanto deve diminuire la misura del lato di un triangolo equilatero che è di 43cm affinché il perimetro sia di 96cm. [11cm]
[:it]
In questi esercizi bisogna sapere:
Esercizi per il 6
| 6.1. |
|
| 6.2. |
Esercizi per il 7
7.1. 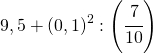 |
|
| 7.2. |
Esercizio per l’8
| 8.1. |
Esercizi 9/10
| 9.1. |
|
10.1. ![Rendered by QuickLaTeX.com \left[\left(2-\cfrac{3}{5}:2,25\right):\left(0,0\bar{7}+\cfrac{1}{15}\right)\right]\cdot\cfrac{5}{108}+0,0\bar{3}:\left[\left(1,\overline{6}-\cfrac{1}{7}\right):\left(1+\cfrac{25}{7}\right)\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-1648f6595fab6f64d3c415d31786b547_l3.png) |
[:en]a) ![]() Risultato:
Risultato:![]()
b) ![]() Risultato:
Risultato:![]()
c) 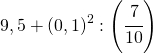 Risultato:
Risultato:![]()
d) ![]() Risultato:
Risultato:![]()
e) ![]() Risutato:
Risutato: ![]()
f) ![]() Ris:
Ris: ![]()
g) ![Rendered by QuickLaTeX.com \left[\left(2-\cfrac{3}{5}:2,25\right):\left(0,0\bar{7}+\cfrac{1}{15}\right)\right]\cdot\cfrac{5}{108}+0,0\bar{3}:\left[\left(1,\overline{6}-\cfrac{1}{7}\right):\left(1+\cfrac{25}{7}\right)\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-1648f6595fab6f64d3c415d31786b547_l3.png) Risultato:
Risultato: ![]() [:de]a)
[:de]a) ![]() Risultato:
Risultato:![]()
b) ![]() Risultato:
Risultato:![]()
c) 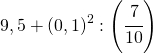 Risultato:
Risultato:![]()
d) ![]() Risultato:
Risultato:![]()
e) ![]() Risutato:
Risutato: ![]()
f) ![]() Ris:
Ris: ![]()
g) ![Rendered by QuickLaTeX.com \left[\left(2-\cfrac{3}{5}:2,25\right):\left(0,0\bar{7}+\cfrac{1}{15}\right)\right]\cdot\cfrac{5}{108}+0,0\bar{3}:\left[\left(1,\overline{6}-\cfrac{1}{7}\right):\left(1+\cfrac{25}{7}\right)\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-1648f6595fab6f64d3c415d31786b547_l3.png) Risultato:
Risultato: ![]() [:]
[:]
Le equazioni di secondo grado sono il primo passo verso la maturità della conoscenza della matematica. In tutti i cicli d’istruzione durante il primo massimo secondo anno delle superiore lo si affronta con sicurezza e la maturità delle persone fa sì che tale argomento non sia assolutamente così ostico.
Ecco il metodo più comune con il quale si risolvono.
Data la seguente equazione:
![]()
il fatto che sia di secondo grado l’incognita ![]() significa che avrò due soluzioni.
significa che avrò due soluzioni.
Le soluzioni sono:
![]()
ma perchè?
La dimostrazione è più semplice di quello che non si pensi.
Si tenga presente il prodotto notevole ![]()
![]() moltiplico entrambi i membri per
moltiplico entrambi i membri per ![]() e si ha:
e si ha:
![]() adesso sommo ad entrambi i membri
adesso sommo ad entrambi i membri ![]() e si ha:
e si ha:
![]() ma il primo membro è esattamente un quadrato del binomio
ma il primo membro è esattamente un quadrato del binomio ![]() e si ha:
e si ha:
![]() risolvendo il quadrato a sinistra ho esattamente due soluzione una positiva ed una negativa:
risolvendo il quadrato a sinistra ho esattamente due soluzione una positiva ed una negativa:
![]()
risolvendola in funzione dell’incognita ![]() ho:
ho:
![]()
che è proprio quella di partenza.
ESPONENZIALI
Il fenomeno del deterioramento del cibo segue una curva esponenziale. Il valore che si utilizza per misurare l’intensità del suono è il decibel. Due fenomeni che per essere descritti richiedono una conoscenza seppur intuitiva degli esponenziali e dei logaritmi.
In particolare la funzione esponenziale è del seguente tipo:
![]()
E’ in uso comune utilizzare però la seguente funzione esponenziale utilizzando come base non un numero qualunque ![]() ma la lettera
ma la lettera ![]() che si chiama numero di nepero o di Eulero che approfondì alcune sue proprietà e vale
che si chiama numero di nepero o di Eulero che approfondì alcune sue proprietà e vale
![]()
Una delle prime proprietà che balzano all’occhio è che la derivata della funzione esponenziale è ancora essa stessa.
![]()
la sua derivata prima diventa:
![]() ossia è l’unica funzione grazie alla quale
ossia è l’unica funzione grazie alla quale
![]()
Il grafico è:
Ma se il numero ![]() è da tutti conosciuto come quel numero tramite il quale si riesce a determinare la lunghezza di una circonferenza o l’area del cerchio, come faccio a calcolare e?
è da tutti conosciuto come quel numero tramite il quale si riesce a determinare la lunghezza di una circonferenza o l’area del cerchio, come faccio a calcolare e?
![]()
con ![]()
ad esempio:
![]()
LOGARITMI
Sono stati utilizzati moltissimo nell’ambito economico per calcolare ad esempio nel caso della capitalizzazione composta il tempo necessario affinché si sia realizzato un certo montante partendo da un opportuno capitale ad un particolare tasso.
Ossia si parte dalla formula che riassume tutta la capitalizzazione composta:
![]()
per poi arrivare alla formula inversa:
![]()
Tale formula viene utilizzata moltissimo già a metà del 1500 quando gli scambi commerciali richiedevano di conoscere il tempo necessario per avere un certo guadagno.
Partendo però dall’inzio:
![]()
allora il logaritmo è definito come:
![]() con b argomento del logaritmo e con
con b argomento del logaritmo e con ![]() il logaritmo naturale o di eulero/nepero.
il logaritmo naturale o di eulero/nepero.
Il grafico risulta:
La derivata del logaritmo (si può dimostrare) vale:
![]()
18. ![]() Come nell’esercizio 15) conviene esprimere la funzione precedente come:
Come nell’esercizio 15) conviene esprimere la funzione precedente come:
![]()
adesso procedo con la derivata prima:
![]()
in conclusione:
![]()
19. ![]() nel punto P(0;-30)
nel punto P(0;-30)
il primo passo è sviluppare la moltiplicazione tra binomi:
![]()
il punto P appartiene?
![]()
il punto P appartiene alla retta.
![]()
![]()
![]() sostituisco q e risulta:
sostituisco q e risulta:
![]() quindi
quindi ![]()
La retta tangente risulta
![]()
20. ![]() nel punto P(1;1)
nel punto P(1;1)
il punto P appartiene alla curva?
![]()
il punto P non appartiene alla retta!
Bisogna seguire il seguente procedimento:
Retta passante per il punto P
![]() ordinandola ho
ordinandola ho ![]() metto in sistema il fascio di rette e la curva e poi pongo a zero il determinante.
metto in sistema il fascio di rette e la curva e poi pongo a zero il determinante.
![]()
utilizzo il metodo del confronto
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
il discriminante è più piccolo di zero e ciò significa che non esiste alcuna retta passante per P e tangente alla curva.
15. ![]()
per poter applicare la definizione in maniera immediata conviene esprimere la funzione precedente in questa maniera:
![]()
![]()
16. ![]()
prima si sviluppa il prodotto notevole e poi la moltiplicazione:
![]()
![]()
17. tangente alla curva ![]() in P(0;0)
in P(0;0)
il punto P appartiene alla curva?
![]()
P appartiene alla curva.
![]()
![]()
la retta è
![]() in quanto m=0 sostituisco il punto P:
in quanto m=0 sostituisco il punto P:
![]()
la retta tangente è ![]()
11. ![]() non bisogna farsi ingannare dalla seconda parte in quando si ha un denominatore.
non bisogna farsi ingannare dalla seconda parte in quando si ha un denominatore.
Per non cadere in errore è sufficiente dividerlo ossia considerare la seguente funzione:
![]()
in questa forma è più facile effettuare la derivata prima:
![]()
12. ![]() nel punto P(1:12)
nel punto P(1:12)
verifico che il punto P appartenga alla curva:
![]()
![]() il punto P appartiene alla curva
il punto P appartiene alla curva
Calcolo la derivata prima della curva:
![]()
![]()
la retta quindi è ![]() per determinare q sostituisco il punto P
per determinare q sostituisco il punto P
![]() da cui
da cui ![]()
L’equazione della retta tangente è:
![]()
13. ![]() nel punto P(0;4)
nel punto P(0;4)
P appartiene alla curva?
![]()
Sì, P appartiene alla curva.
![]()
Significa che la retta tangente alla retta è la retta stessa.
Avendo dato come definizione di derivata la pendenza della retta tangente ad una curva, inevitabilmente l’affermazione precedente è vera.
Una cosa è fondamentale:
LA DERIVATA FORNISCE L’INCLINAZIONE DELLA CURVA IN UN OPPORTUNO PUNTO DELLA CURVA
ESSERE TANGENTI IN UN PUNTO DELLA CURVA SIGNIFICA CALCOLARE IN QUEL PRECISO PUNTO QUANTO VALE L’INCLINAZIONE DELLA CURVA
LA RETTA TANGENTE IN UN PUNTO POTREBBE BENISSIMO INTERSECARE LA CURVA IN UNA ALTRO PUNTO MA QUELLO CHE INTERESSA E’ L’INCLINAZIONE DELLA RETTA NEL PUNTO PRESO IN CONSIDERAZIONE.
Vedasi questo esempio:
Si vuole calcolare la retta tangente tangente alla curva:
![]() nel punto P(0:-1)
nel punto P(0:-1)
è la retta ![]()
14. Retta tangente alla curva ![]() nel punto P(3;4)
nel punto P(3;4)
il punto P appartiene alla retta?
No!
![]()
![]()
NON ESISTE alcuna retta che passa per P(3:4) e che sia tangente alla retta di partenza ossia con coefficiente angolare ![]() .
.
OSSERVAZIONE
Si potrebbe pensare che la retta x=3 sia proprio la retta tangente ma è sì una retta che tocca la retta in un punto, come pure tutte quelle appartenenti al fascio di rette ![]() , ma NESSUNA presenta la stessa inclinazione della retta
, ma NESSUNA presenta la stessa inclinazione della retta ![]() o meglio tangente.
o meglio tangente.
E’ il caso più semplice di ordinamento che si conosca. E’ il metodo meno efficiente in termini di tempi di risoluzione ma è il più intuitivo. Tradotto significa bolle ossia si comporta come le bollicine di una bottiglia di acqua minerale che dal basso risalgono verso l’alto. L’algoritmo è il seguente:
Il primo elemento del vettore si confronta con l’elemento successivo se è maggiore si scambia do posto.
Se arrivato al secondo posto è ancora maggiore del terzo si scambia e così via fino ad arrivare all’ultimo posto.
Si riprende dall’inizio confrontando nuovamente il primo posto con il secondo fino ad arrivare al penultimo in quanto l’ultimo è già ordinato.
Ecco un esempio di un semplice vettore formato da cinque elementi non ordinati:
5 4 3 2 1
PRIMA FASE
5>4 scambio –> 4 5 3 2 1
5>3 scambio –> 4 3 5 2 1
5 >2 scambio –> 4 3 2 5 1
5>1 scambio –> 4 3 2 1 5
SECONDA FASE (si ferma ad un punto inferiore rispetto al precedente)
4>3 scambio –> 3 4 2 1 5
4>2 scambio –> 3 2 4 1 5
4>1 scambio –> 3 2 1 4 5
TERZA FASE
3 > 2 scambio –> 2 3 1 4 5
3> 1 scambio –> 2 1 3 4 5
QUARTA FASE
2 > 1 scambio 1 2 3 4 5
STOP
Il numero delle fasi è sempre uguale al numero di elementi meno.
Come esercizio è utile provare ad implementarlo (suggerimento sono due cicli uno all’interno dell’altro).
Ecco le soluzioni:
1.![]() .
.
![]() .
.
![]() o meglio
o meglio ![]() .
.
2. ![]()
![]() semplificando il numeratore con il denominatore diventa:
semplificando il numeratore con il denominatore diventa:
![]()
![]() o meglio
o meglio ![]()
3. ![]()
![]()
![]() che semplificandola ulteriormente diventa
che semplificandola ulteriormente diventa
![]()
4. ![]()
![]()
![]()
5.![]()
![]() che semplificando diventa
che semplificando diventa
![]()
![]() che semplilficato diventa
che semplilficato diventa
![]()
6.![]()
![]()
![]()
7.![]()
![]()
![]()
8. ![]()
![]() che scritto in maniera semplificata
che scritto in maniera semplificata
![]()
![]() che semplificata risulta
che semplificata risulta
![]()
9.![]()
![]()
![]()
10. Retta tangente a ![]() nel punto P(1:5)
nel punto P(1:5)
Il punto P appartiene alla curva infatti:
![]()
allora
![]() ossia meglio
ossia meglio ![]() adesso alla x sostituisco la coordinata x del punto P ed ho
adesso alla x sostituisco la coordinata x del punto P ed ho ![]()
Il coefficiente angolare della retta è m=5.
La retta è ![]() . Devo trovare ancora q sostituendo le coordinate del punto P:
. Devo trovare ancora q sostituendo le coordinate del punto P:
![]() e risolvendola rispetto all’incognita q–>
e risolvendola rispetto all’incognita q–>
![]()
la retta tangente è ![]()