
Salvador Dalì
ESPONENZIALI
Il fenomeno del deterioramento del cibo segue una curva esponenziale. Il valore che si utilizza per misurare l’intensità del suono è il decibel. Due fenomeni che per essere descritti richiedono una conoscenza seppur intuitiva degli esponenziali e dei logaritmi.
In particolare la funzione esponenziale è del seguente tipo:
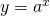
E’ in uso comune utilizzare però la seguente funzione esponenziale utilizzando come base non un numero qualunque  ma la lettera
ma la lettera  che si chiama numero di nepero o di Eulero che approfondì alcune sue proprietà e vale
che si chiama numero di nepero o di Eulero che approfondì alcune sue proprietà e vale
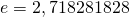
Una delle prime proprietà che balzano all’occhio è che la derivata della funzione esponenziale è ancora essa stessa.
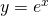
la sua derivata prima diventa:
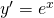 ossia è l’unica funzione grazie alla quale
ossia è l’unica funzione grazie alla quale
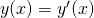
Il grafico è:
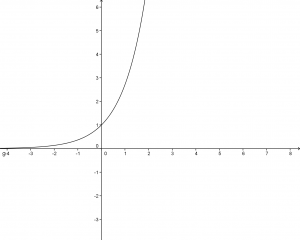
Esponenziale
Ma se il numero 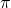 è da tutti conosciuto come quel numero tramite il quale si riesce a determinare la lunghezza di una circonferenza o l’area del cerchio, come faccio a calcolare e?
è da tutti conosciuto come quel numero tramite il quale si riesce a determinare la lunghezza di una circonferenza o l’area del cerchio, come faccio a calcolare e?
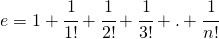
con 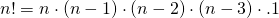
ad esempio:
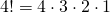
LOGARITMI
Sono stati utilizzati moltissimo nell’ambito economico per calcolare ad esempio nel caso della capitalizzazione composta il tempo necessario affinché si sia realizzato un certo montante partendo da un opportuno capitale ad un particolare tasso.
Ossia si parte dalla formula che riassume tutta la capitalizzazione composta:
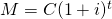
per poi arrivare alla formula inversa:
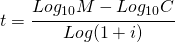
Tale formula viene utilizzata moltissimo già a metà del 1500 quando gli scambi commerciali richiedevano di conoscere il tempo necessario per avere un certo guadagno.
Partendo però dall’inzio:
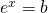
allora il logaritmo è definito come:
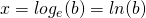 con b argomento del logaritmo e con
con b argomento del logaritmo e con 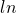 il logaritmo naturale o di eulero/nepero.
il logaritmo naturale o di eulero/nepero.
Il grafico risulta:
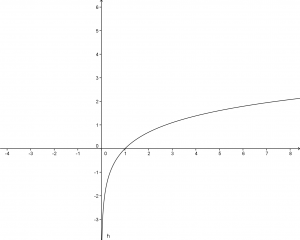
logaritmo
La derivata del logaritmo (si può dimostrare) vale:
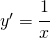
![]() (ZERO).
(ZERO).![]()
![]()
![]()
![]() ossia
ossia ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


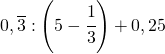
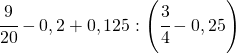

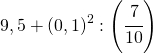
![Rendered by QuickLaTeX.com \left[\left(2-\cfrac{3}{5}:2,25\right):\left(0,0\bar{7}+\cfrac{1}{15}\right)\right]\cdot\cfrac{5}{108}+0,0\bar{3}:\left[\left(1,\overline{6}-\cfrac{1}{7}\right):\left(1+\cfrac{25}{7}\right)\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-1648f6595fab6f64d3c415d31786b547_l3.png)



