SCIENZE E TECNOLOGIE INFORMATICHE

Gino Severini

1) Il primo passo è verificare che il punto appartenga o meno alla curva fornita. Tale fatto fa sì che il problema si sviluppi utilizzando il significato geometrico della derivata o meno.

Nel caso specifico si nota che sostituendo alla x il valore 0 (zer0) ed alla y il valore 1 (uno) si ha:

ossia:

che non essendo un’identità dimostra il fatto che il punto P non appartiene alla curva.

Non ha senso quindi calcolare la derivata prima della curva data.

Allora per determinare l’equazione della retta tangente eseguo i seguenti passi:

1.a) per determinare l’equazione delle rette passanti per il punto P  utilizzo la seguente forma:

nella quale sostituisco il valore dell’ordinata e dell’ascissa del punto P e diventa:

ossia sviluppando i calcoli ho che mettendola in forma canonica diventa:

ESSA RAPPRESENTA UN FASCIO DI RETTE (proprio) TUTTE PASSANTI PER IL PUNTO FORNITO

Adesso devo mettere in sistema la mia curva con il fascio di rette e PONENDO IL DETERMINANTE A ZERO trovo il valore di m delle rette tangenti alla curva data.

applico il metodo risolutivo del confronto (validissimo in questo caso e mi trovo la seguente equazione:

quindi ordinandola rispetto alla x ho:

adesso raggruppando la x e sommando i coefficienti senza x ho

Adesso NON DEVO RISOLVERE L’EQUAZIONE MA PRENDERE SOLO IL DETERMINANTE

ricordarsi che

per cui sostituendo ho: ossia   che ordinandola per l’incognita m diventa:

Applicando la formula risolutiva dell’equazione di secondo grado

si ha:

e si nota subito che il determinante è più piccolo di zero.

Cosa significa? Che nessuna retta appartenente al fascio sarà MAI tangente alla curva data (in questo caso è una parabola).

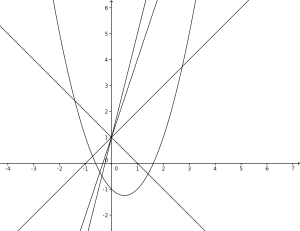
Graficamente la soluzione appare immediata:

Ossia nessuna retta appartenente al fascio con centro in P(0;1) sarà mai tangente alla mia parabola.

Giacomo Balla – 1912 – “Bambina che corre sul balcone”

Date le seguenti curve, determinare l’equazione della retta tangente passante per il punto specificato. Verificare che il punto dato appartenga alla curva. In caso contrario vedasi le soluzioni per determinare il corretto metodo da seguire.

1. nel punto P(0;1)  [soluzione]

2. nel punto P(1;-1) [soluzione]

3. nel punto P(0;0) [soluzione]

Fortunato Depero

Queste sono le soluzioni agli esercizi precedenti:

1.

e sviluppando le moltiplicazioni e sapendo che qualunque numero elevato alla zero dà o (zero) si ha:

2. 

x elevato alla uno non si scrive per cui il risultato diventa:

3.

4.

A prescindere dal segno dell’esponente la regola può essere applicata pedissequamente:

E’ un uso comune non mantenere l’esponente della variabile negativa per cui la forma corretta è la seguente:

5.

DA RICORDARSI SEMPRE CHE LA DERIVATA PRIMA DI UNA COSTANTE E’ SEMPRE ZERO

6.

che semplificando i 3 diventa semplicemente

7.

che seguendo il consiglio precedente sarebbe meglio scriverla come:

non è ancora corretta e quindi si esegue il seguente passo:

8.

Umberto Boccioni

Determinare la derivata prima delle seguenti funzioni polinomiali.

1. .

2. .

3. .

4. .

5. .

6. .

Questa è una funzione irrazionale considerando il fatto che vi è la radice

7..

la stessa funzione può essere scritta come:

.

8. .

Provare a risolverle e poi eventualmente andare alle soluzioni.

Wassily Kandinsky

Dato il prodotto di due funzioni che per comodità indicherò con u e v, per calcolare la loro derivata dovrò seguire il seguente procedimento:

Utilizzo sempre l’approccio NSA ho:

y + dy = (u +du)(v+dv)

sviluppo il prodotto:

y + dy = uv+udv+vdu+dudv

y e uguale uv per  cui ho:

uv + dy = uv + udv + vdu + dudv

elimino uv che sono uguali ed opposti ed ho:

dy =  udv + vdu + dudv

adesso divido per dx a destra e sinistra ed ho:

.

ma l’ultimo termine essendo infinitesimo si può scartare per poi avere alla fine:

REGOLA DI LEIBNIZ

conosciuta anche in questa forma:

se

y = f(x)g(x)

y’=f'(x)g(x)+f(x)g'(x)

Giorgio De Chirico

Determinare la retta tangente ad una curva è solo la conseguenza immediata del riuscire a calcolare la derivata prima di una qualunque curva.

Il vantaggio che se ne trae immediatamente è quello di evitare di dover risolvere un sistema di equazioni, a volte di non semplice risoluzione, e il successivo studio del discriminante.

Sviluppo il seguente esercizio partendo solo dalle conoscenze di derivata e di retta passante per un punto appartenente alla curva data.

Si abbia la curva di equazione:

(1.0)  .

ed il punto P(1;6) che appartiene alla curva precedente.

COME FACCIO A VERIFICARE CHE QUESTO PUNTO APPARTIENE PROPRIO ALLA CURVA?

E’ sufficiente sostituire il valore della prima coordinata all’equazione (1.0) e verificare che si abbia un’identità. Infatti:

che è proprio un’identità

calcolo la derivata prima della  (1.0)

(1.1) .

Adesso sostituisco il valore della prima coordinata del punto P che è 1 nella (1.1) ossia nella derivata prima (y’) ed ho:

y'(1) = 4+6+2 = 12

il coefficiente angolare della retta tangente m=12

Per trovare adesso l’intercetta o l’ordinata all’origine o meglio ancora la q della retta

y=12x+q

è sufficiente sostituire i valori delle coordinate del punto P e si ha:

6 = 12 + q

che risolta dà q=-6

Quindi l’equazione della retta tangente alla curva (1.0) nel punto P(1;6)  è